Question

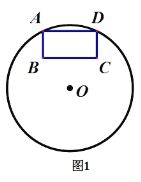
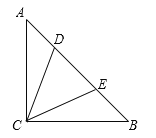
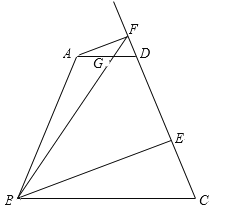
【题目】四边形ABCD是⊙O的圆内接四边形，线段AB是⊙O的直径，连结AC.BD．点H是线段BD上的一点，连结AH、CH，且∠ACH＝∠CBD，AD＝CH，BA的延长线与CD的延长线相交与点P．

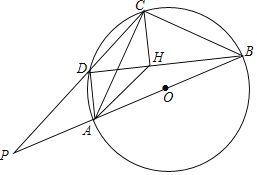
（1）求证：四边形ADCH是平行四边形；

（2）若AC＝BC，PB＝PD，AB+CD＝2（+1）

①求证：△DHC为等腰直角三角形；②求CH的长度．

Answer 1

【答案】（1）见解析；（2）①见解析；②．

【解析】

（1）由圆周角的定理可得，可证，由一组对边平行且相等的是四边形是平行四边形可证四边形是平行四边形；

（2）①由平行线的性质可证，由，可证为等腰直角三角形；

②通过证明，可得，可得，通过证明，可得，可得，可求，由等腰直角三角形的性质可求的长度．

证明：（1），

，且

四边形是平行四边形

（2）①是直径

，且

，

，且

，且

为等腰直角三角形；

②四边形是的圆内接四边形，

，且

，且，

，，

，

，且为等腰直角三角形