题目内容
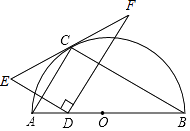
【题目】如图，已知矩形ABCD的两条对角线相交于点O，过点A作AG⊥BD分别交BD、BC于点G、E．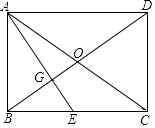 
（1）求证：BE2=EGEA；
（2）连接CG，若BE=CE，求证：∠ECG=∠EAC．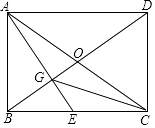 
【答案】
（1）证明：（1）∵四边形ABCD是矩形，
∴∠ABC=90°，
∵AE⊥BD，
∴∠ABC=∠BGE=90°，
∵∠BEG=∠AEB，
∴△ABE∽△BGE，
∴ 
，
∴BE2=EGEA；
（2）解：由（1）证得BE2=EGEA，
∵BE=CE，
∴CE2=EGEA，
∴ 
= 
，
∵∠CEG=∠AEC，
∴△CEG∽△AEC，
∴∠ECG=∠EAC．
【解析】（1）由四边形ABCD是矩形，得到∠ABC=90°，得到∠ABC=∠BGE=90°，根据相似三角形的性质即可得到结论；（2）由（1）证得BE2=EGEA，推出△CEG∽△AEC，根据相似三角形的性质即可得到结论．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某商场经营某种品牌的玩具，进价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价（元） | x |
销售量y（件） | |
销售玩具获得利润w（元） |
（2）在（1）问条件下，若商场获得了8000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具车规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌服装获得的最大利润是多少？
