题目内容
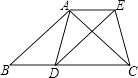
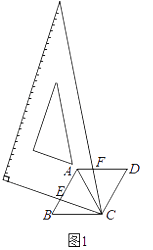
【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
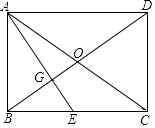
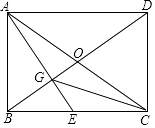
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF= ![]() AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由.
【答案】
(1)
①证明:如图1中,
∵四边形ABCD 是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠BCF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
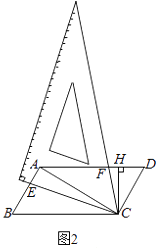
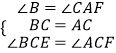 ,
,
∴△BCE≌△ACF.
②如图1中,
∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
∴AE+AF=AC.
(2)
证明:如图2中,
设DH=x,由题意CD=2x,CH= ![]() x.
x.
∴AD=2AB=4x,AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC= ![]() =2
=2 ![]() x,
x,
∴AC2+CD2=16x2,AD2=16x2,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°=∠ACH,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴ ![]() =
= ![]() =2,
=2,
∴AE=2FH.
(3)
结论正确.
理由:如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,
易知AC=2 ![]() x,
x,
∴AF=3x﹣a,
∴AE+2AF=2a+2(3x﹣a)=6x= ![]() AC.
AC.
【解析】(1)①首先证明△ABC,△ACD都是等边三角形,根据ASA即可证明.②利用①中结论,即可证明.(2)首先利用勾股定理逆定理证明△ACD是直角三角形,再证明△ACE∽△HCF,即可推出 ![]() =
= ![]() =2.(3)利用代数法证明,如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,易知AC=2
=2.(3)利用代数法证明,如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,易知AC=2 ![]() x,AF=3x﹣a,即可得出AE+2AF=2a+2(3x﹣a)=6x=
x,AF=3x﹣a,即可得出AE+2AF=2a+2(3x﹣a)=6x= ![]() AC.
AC.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】为了合理利用电力资源,缓解用电紧张状况,我国电力部门出台了使用“峰谷电”的政策及收费标准(见下表).
用电时间段 | 收费标准 | |
峰电 | 08:00—22:00 | 0.56元/千瓦时 |
谷电 | 22:00—08:00 | 0.28元/千瓦时 |
已知王老师家4月份使用“峰谷电”95千瓦时,缴电费43.40元,问王老师家4月份“峰电”和“谷电”各用了多少千瓦时?设王老师家4月份“峰电”用了x千瓦时,“谷电”用了y千瓦时,根据题意,列方程组得_____.