题目内容
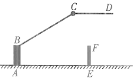
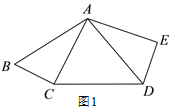
【题目】如图 1,在五边形 ABCDE 中,∠E=90°,BC=DE.连接 AC,AD, 且 AB=AD,AC⊥BC.
(1)求证:AC=AE;
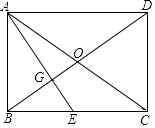
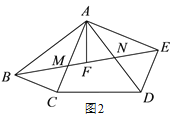
(2)如图 2,若∠ABC=∠CAD,AF 为 BE 边上的中线,求证:AF⊥CD;
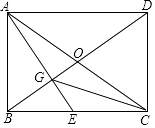
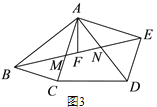
(3)如图 3,在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为_____.
【答案】(1)见解析;(2)见解析;(3)42
【解析】
(1)由已知可得Rt△ABC≌Rt△ADE(HL),可得结论;
(2)延长 AF,BC 交于点 G,连接CG,可得∠G=∠EAG,可证明得:△AEF≌△GBF(AAS),可得AE=BG,∠ABG=∠CAD,可证明得△ABG≌△DAC(SAS),∠G=∠ACD,可得结论;
(3) 在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为42.
(1)∵AC⊥BC,,
∴∠ACB=90°=∠E. 在 Rt△ABC 和 Rt△ADE 中,
AB AD,BC DE,
∴Rt△ABC≌Rt△ADE(HL),
∴AC=AE.
(2)延长 AF,BC 交于点 G,
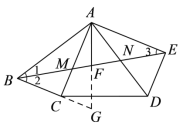
∵∠ABC=∠CAD,∠BAC=∠DAE,
∴∠CAD+∠DAE=∠ABC+∠BAC=90°=∠ACB,,
∴BG∥AE,
∴∠G=∠EAG,
在△AEF 和△GBF 中,
AFE GFB,EAF G,EF BF,
∴△AEF≌△GBF(AAS),
∴AE=BG,
∵AC= AE,
∴BG=AC.
∵∠2=∠3,
又∠ABG=∠1+∠2,
∠CAD=∠BAD+∠CAE-∠BAE,,
=180-∠BAE=180-(180-∠1-∠3)=∠1+∠3,
∴∠ABG=∠CAD,
在△ABG 和△DAC 中,
AB AD,ABG DAC,BG AC,
∴△ABG≌△DAC(SAS),
∴∠G=∠ACD,
∵∠ACG=∠ACB= 90° 即:∠ACD+∠GCD=90°,
∴∠G+∠GCD=90°,
∴AF⊥CD;
(3)在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为42 .

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案