题目内容
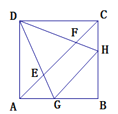
【题目】在正方形ABCD中,点G在AB上,点H在BC上,且∠GDH=45°,DG、DH分别与对角线AC交于点E、F,则线段AE、EF、FC之间的数量关系为_______ .
【答案】![]()
【解析】
把△DCH绕点D顺时针旋转90°至△DAH’,在GH上截取GM=AG,连接EM、FM,
证明△DH’G≌△DHG,从而证明MH=CH,再证明△AGE≌△MGE、△CHF≌△MHF,从而得到∠EMF=90°,即可证明结论.
证明:将△DCH绕点D顺时针旋转90°至△DAH’,在GH上截取GM=AG,连接EM、FM,
∵∠ADC=90°,∠GDH=45°,
∴∠ADG+∠CDH=45°,
∵∠ADH’=∠CDH,
∴∠ADG+∠ADH’=45°,即∠GDH’ =45°,
∴∠GDH=∠GDH’,
又DG=DG,DH=DH’,
∴△DH’G≌△DHG,
∴H’G=HG,∠DGH’=∠DGH,∠DHG =∠DH’G=∠DHC,
又∵GM=AG,
∴MH=AH’=CH,
∵GM=AG,∠DGH’=∠DGH,EG=EG,
∴△AGE≌△MGE,
∴AE=ME,∠EMG=∠EAG,
∵MH=CH,∠DHG =∠DHC,FH=FH,
∴△CHF≌△MHF,
∴CF=MF,∠FCH=∠FMH,
∵四边形ABCD为正方形,
∴∠EAG=∠FCH=45°,
∴∠EMG=∠FMH=45°,
∴∠EMF=90°,
∴![]() ,
,
∴![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度![]() (
(![]() )与它的飞行时间
)与它的飞行时间![]() (
(![]() )满足二次函数关系,
)满足二次函数关系,![]() 与
与![]() 的几组对应值如下表所示:
的几组对应值如下表所示:

|
|
|
|
|
| … |
|
|
|
|
|
| … |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写
的函数解析式(不要求写![]() 的取值范围)
的取值范围)
(2)问:小球的飞行高度能否达到![]() ?请说明理由
?请说明理由