题目内容
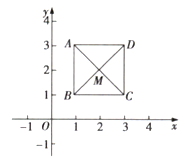
【题目】如图，已知正方形ABCD的顶点
，
，
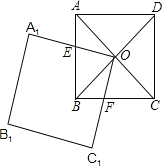
，规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位长度”为一次变换，如此这样，连续经过2019次变换后，正方形ABCD的对角线的交点M的坐标为（ ）
A.
B.
C.
D.
【答案】C
【解析】
由正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），然后根据题意求得第1次、2次、3次变换后的点M的对应点的坐标，即可得规律：第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），继而求得把正方形ABCD连续经过2019次这样的变换得到点M的坐标．
解：∵正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1）．
∴点M的坐标为（2，2），
根据题意得：第1次变换后的点M的对应点的坐标为（2-1，-2），即（1，-2），
第2次变换后的点M的对应点的坐标为：（2-2，2），即（0，2），
第3次变换后的点M的对应点的坐标为（2-3，-2），即（-1，-2），
第n次变换后的点M的对应点的为：当n为奇数时为（2-n，-2），当n为偶数时为（2-n，2），
∴连续经过2019次变换后，点M的坐标变为（-2017，-2）．
故选：C．
练习册系列答案
相关题目
