题目内容
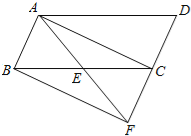
【题目】如图1,△ABC中,AB=AC=6,BC=4,点D、E分别在边AB、AC上,且AD=AE=1,连接DE、CD,点M、N、P分别是线段DE、BC、CD的中点,连接MP、PN、MN.
(1)求证:△PMN是等腰三角形;
(2)将△ADE绕点A逆时针旋转,
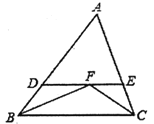
①如图2,当点D、E分别在边AC两侧时,求证:△PMN是等腰三角形;
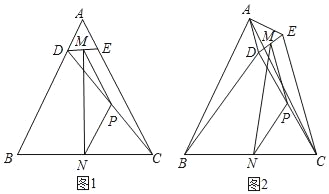
②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,请直接写出此时BD的长.
【答案】(1)见解析;(2)①见解析;②![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论PM=PN;
BD,进而判断出BD=CE,即可得出结论PM=PN;
(2)①先证明△ABD≌△ACE,得BD=CE,同理根据三角形中位线定理可得结论;
②如图4,连接AM,计算AN和DE、EM的长,如图3,证明△ABD≌△CAE,得BD=CE,根据勾股定理计算CM的长,可得结论
(1)如图1,∵点N,P是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∴△PMN是等腰三角形;
(2)①如图2,∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∵点M、N、P分别是线段DE、BC、CD的中点,
∴PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形;
②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,如图3,
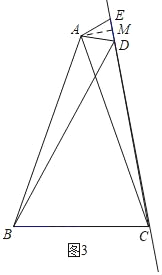
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△CAE,
∴BD=CE,
如图4,连接AM,
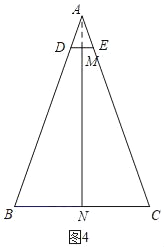
∵M是DE的中点,N是BC的中点,AB=AC,
∴A、M、N共线,且AN⊥BC,
由勾股定理得:AN=![]() =4
=4![]() ,
,
∵AD=AE=1,AB=AC=6,
∴![]() =
=![]() ,∠DAE=∠BAC,
,∠DAE=∠BAC,
∴△ADE∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴AM=![]() ,DE=
,DE=![]() ,
,
∴EM=![]() ,
,
如图3,Rt△ACM中,CM=![]() =
=![]() =
=![]() ,
,
∴BD=CE=CM+EM=![]() .
.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案