题目内容
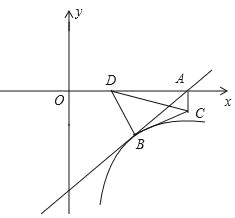
【题目】如图,在平面直角坐标系中,直线y=kx﹣10经过点A(12,0)和B(a,﹣5),双曲线y=![]() 经过点B.
经过点B.
(1)求直线y=kx﹣10和双曲线y=![]() 的函数表达式;
的函数表达式;
(2)点C从点A出发,沿过点A与y轴平行的直线向下运动,速度为每秒1个单位长度,点C的运动时间为t(0<t<12),连接BC,作BD⊥BC交x轴于点D,连接CD,
①当点C在双曲线上时,求t的值;
②在0<t<6范围内,∠BCD的大小如果发生变化,求tan∠BCD的变化范围;如果不发生变化,求tan∠BCD的值.
③当DC=![]() 时,请直接写出t的值.
时,请直接写出t的值.
【答案】(1)y=﹣![]() ;(2)①
;(2)①![]() ,②当0<t<6时,点D在线段OA上,∠BCD的大小不变.
,②当0<t<6时,点D在线段OA上,∠BCD的大小不变.![]() ,③t=
,③t=![]() 或
或![]() (舍弃);综上所述,满足条件的t的值为t=
(舍弃);综上所述,满足条件的t的值为t=![]() 或
或![]() s.
s.
【解析】
(1)理由待定系数法即可解决问题;
(2)①求出点C坐标即可解决问题;
②如图1中,设直线AB交y轴于M,则M(0,﹣10),A(12, 0),取CD的中点K,连接AK、BK.证明A、D、B、C四点共圆,可得∠DCB=∠DAB,得出tan∠DCB=tan∠DAB=![]() ,即可解决问题;
,即可解决问题;
③分两种情形分别构建方程即可解决问题;
(1)∵直线y=kx﹣10经过点A(12,0)和B(a,﹣5),
∴12k﹣10=0,
∴k=![]() ,
,
∴y=![]() x﹣10,
x﹣10,
∴﹣5=![]() a﹣10,
a﹣10,
∴a=6,
∴B(6,﹣5),
∵双曲线y=![]() 经过点B,
经过点B,
∴m=﹣30,
∴双曲线解析式为y=﹣![]() .
.
(2)①∵AC∥y轴,
∴点C的横坐标为12,
y=﹣![]() =﹣
=﹣![]() ,
,
∴C(12,﹣![]() ),
),
∴AC=![]() ,
,
∴点C在双曲线上时,t的值为![]() .
.
③如图2中,当t<5时,作BM⊥OA于M,CN⊥BM于N.
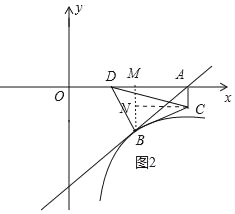
则△CNB∽△BMD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DM=![]() (5﹣t),
(5﹣t),
∴AD=6+![]() (5﹣t),
(5﹣t),
∵DC=![]() ,
,
∴[6+![]() (5﹣t)]2+t2=(
(5﹣t)]2+t2=(![]() )2,
)2,
解得t=![]() 或
或![]() (舍弃).
(舍弃).
当t>5时,同法可得:[6﹣![]() (t﹣5)]2+t2=(
(t﹣5)]2+t2=(![]() )2,
)2,
解得t=![]() 或
或![]() (舍弃),
(舍弃),
综上所述,满足条件的t的值为t=![]() 或
或![]() s.
s.

 小学教材完全解读系列答案
小学教材完全解读系列答案