题目内容
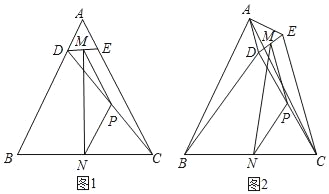
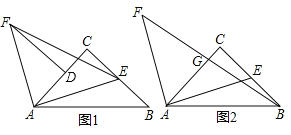
【题目】如图,![]() 中,
中,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,那么下列结论:
,那么下列结论:
①![]() 是等腰三角形;②
是等腰三角形;②![]() ;
;
③若![]() ,
,![]() ;④
;④![]() .
.
其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
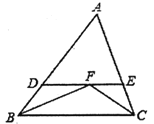
根据角平分线的定义和平行线的性质可得∠DBF =∠DFB,∠ECF=∠EFC,然后利用等角对等边即可得出DB=DF,EF=EC,从而判断①和②;利用三角形的内角和定理即可求出∠ABC+∠ACB,然后利用角平分线的定义和三角形的内角和定理即可求出∠BFC,从而判断③;然后根据∠ABC不一定等于∠ACB即可判断④.
解:∵![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,
,
∴∠DBF=∠FBC,∠ECF=∠FCB
∵![]()
∴∠DFB=∠FBC,∠EFC=∠FCB
∴∠DBF =∠DFB,∠ECF=∠EFC
∴DB=DF,EF=EC,
即![]() 是等腰三角形,故①正确;
是等腰三角形,故①正确;
∴DE=DF+EF= BD+CE,故②正确;
∵∠A=50°
∴∠ABC+∠ACB=180°-∠A=130°
∴∠FBC+∠FCB=![]() (∠ABC+∠ACB)=65°
(∠ABC+∠ACB)=65°
∴∠BFC=180°-(∠FBC+∠FCB)=115°,故③正确;
∵∠ABC不一定等于∠ACB
∴∠FBC不一定等于∠FCB
∴BF不一定等于CF,故④错误.
正确的有①②③,共3个
故选B.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目