题目内容
【题目】(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形每组对边的平方和是一个定值.
(从特殊入手)
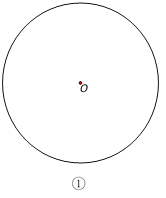
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.请你在图①中补全特殊位置时的图形,并借助于所画图形探究问题的结论.
(问题解决)
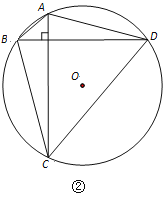
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
【答案】【从特殊入手】证明见解析;【问题解决】AB2+CD2=BC2+AD2=4R2;证明见解析.
【解析】
【从特殊入手】:根据正方形的性质、勾股定理计算;
【问题解决】:根据题意写出已知、求证,作直径DE,连接CE,根据圆周角定理证明∠ADB=∠CDE,得到AB=CE,根据勾股定理计算.
【从特殊入手】
解:如果一个定圆的内接四边形对角线互相垂直,
那么这个四边形的对边平方和是定圆半径平方的4倍.
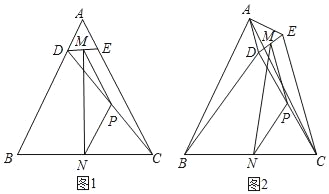
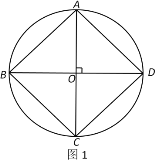
情况一: 如图1,当AC、BD是两条互相垂直的直径时.
则AB2=OA2+ OB2=R2+R2=2R2,
CD2=OC2+ OD2=R2+R2=2R2,
BC2=OC2+ OB2=R2+R2=2R2,
AD2=OA2+ OD2=R2+R2=2R2.
所以AB2+CD2=BC2+AD2=2R2+2R2=4R2.
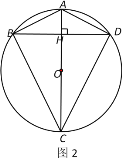
情况二: 如图2,当AC⊥BD,且AC直径时.
根据垂径定理可知:AB=AD,BC=DC.
因为AC是直径,所以∠ABC=∠ADC=90°.
所以AB2+CD2=AD2+CD2=AC2=4R2.
【问题解决】
求证:AB2+CD2=BC2+AD2=4R2
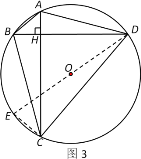
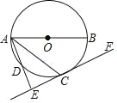
证明:如图3.作直径DE,连接CE.
∵DE是直径,∴∠DCE=90°.
∵![]() 所对的圆周角是∠E与∠DAH,
所对的圆周角是∠E与∠DAH,
∴∠E=∠DAH.
∵∠DAC+∠ADB=90°,∠E+∠CDE=90°,
∴∠ADB=∠CDE.
∴![]() .∴AB=CE.
.∴AB=CE.
∴AB2+CD2=CE2+CD2=DE2=4R2.
同理:BC2+AD2=4R2.

 阅读快车系列答案
阅读快车系列答案【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.