题目内容
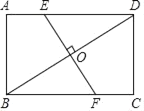
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据已知条件易证∠BFO=∠DEO,∠FBO=∠EDO,OB=OD,再利用AAS证明△BOF≌△DOE即可;(2)连接BE,设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,在Rt△ABE中,根据AB2+AE=BE2,构建方程即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFO=∠DEO,∠FBO=∠EDO,
又∵O是BD中点,
∴OB=OD,
∴△BOF≌△DOE(ASA).
(2)连接BE.
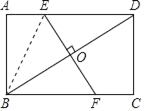
∵EF⊥BD,O为BD中点,
∴EB=ED,
设AE=xcm,由EB=ED=AD﹣AE=(4﹣x)cm,
在Rt△ABE中,AB=3cm,
根据勾股定理得:AB2+AE=BE2,即9+x2=(4﹣x)2,
解得:x=![]() ,
,
∴AE的长是 ![]() cm.
cm.

【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
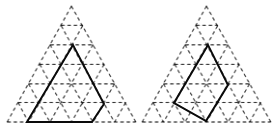
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).
【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.