题目内容
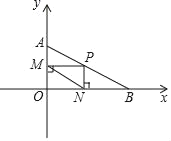
【题目】如图，已知在平面直角坐标系中有两点A（0，1），B（
，0），动点P在线段AB上运动，过点P作y轴的垂线，垂足为点M，作x轴的垂线，垂足为点N，连接MN，则线段MN的最小值为（ ）
A. 1B. C. 
D. 
【答案】D
【解析】
过点P向两坐标轴做垂线与两坐标轴转成的四边形是矩形，根据矩形的对角线相等，只要求出对角线OP的最小值，即可求得MN的最小值，由于P点是AB上的点，当OP⊥AB时，OP最短，由此求得OP的长，即可解决问题.
连接OP，
A（0，1），B（
，0）
∴OA＝1，OB＝
∴AB＝
＝2
∵PM⊥AO，PN⊥OB
∴∠PMO＝∠PNO＝90°
又∵∠ABO＝90°
∴∠AOB＝∠PMO＝∠PNO＝90°
∴四边形PMON是矩形
∴MN＝OP
∴当OP最小时，MN最小
当OP⊥AB时，OP最小
此时有
ABOP＝OAOB
∴ABOP＝OAOB
∴2OP＝1×
∴OP＝
.
故选D．
练习册系列答案
相关题目
