Question

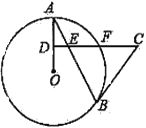
【题目】在△ABC中，D是CB延长线上一点，∠BAD＝∠BAC．

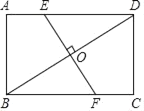
（1）如图，求证：；

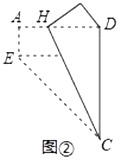
（2）如图，在AD上有一点E，∠EBA＝∠ACB＝120°．若AC＝2BC＝2，求DE的长；

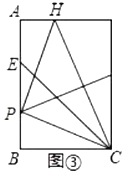
（3）如图，若AB＝AC＝2BC＝4，BE⊥AB交AD于点E，直接写出△BDE的面积．

Answer 1

【答案】(1)见解析；（2）DE＝；（3）

【解析】

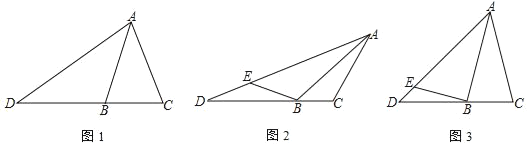
（1）如图1中，作BE⊥AD于E，BF⊥AC于F．利用面积法证明即可．

（2）如图2中，作AH⊥DC交DC的延长线于H．解直角三角形求出AB，再利用相似三角形的性质解决问题即可．

（3）如图3中，作AH⊥BC于H，BM⊥AC于M，EF⊥BD于F．利用面积法求出BM，再利用相似三角形的性质求出BE，BF，EF，DF即可解决问题．

（1）证明：如图1中，作BE⊥AD于E，BF⊥AC于F．

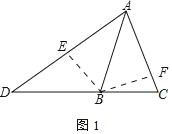
∵∠BAD＝∠BAC，BE⊥AD，BF⊥AC，

∴BE＝BF，

∴，

∴．

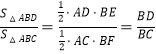（2）解：如图2中，作AH⊥DC交DC的延长线于H．

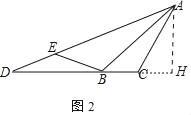
在Rt△ACH中，∵∠AHC＝90°，AC＝2，∠ACH＝60°，

∴CH＝1，AH＝，

在Rt△ABH中，AB＝，

∵∠EAB＝∠BAC，∠ABE＝∠ACB，

∴△EAB∽△BAC，

∴，

∴，

∴AE＝，EB＝，

∵∠ABD＝∠DBE+∠ABE＝∠ACB+∠BAC，∠ABE＝∠ACB，

∴∠DBE＝∠BAC，

∵∠BAC＝∠BAD，

∴∠DBE＝∠BAD，

∵∠D＝∠D，

∴△DEB∽△DBA，

∴，

∴，

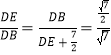∴DE＝．

（3）解：如图3中，作AH⊥BC于H，BM⊥AC于M，EF⊥BD于F．

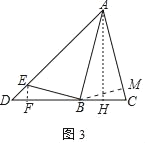
∵AB＝AC＝4，AH⊥BC，

∴BH＝CH＝1，

∴AH＝，

∵BCAH＝ACBM，

∴BM＝，AM＝,

∵∠BAE＝∠BAM，∠ABE＝∠AMB＝90°，

∴△ABE∽△AMB，

∴，

∴BE＝，

由△EFB∽△BHA，

∴，

∴，

EF＝，BF＝，

∵EF∥AH，

∴，

∴，

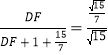∴DF＝，

∴S△BDE＝BDEF＝×（）×＝．