题目内容
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数为a,内部的格点个数为b,则S=![]() a+(b-1).
a+(b-1).
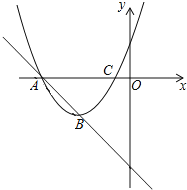
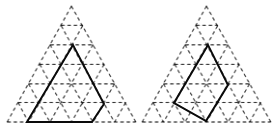
对于正三角形网格中的类似问题也有对应结论:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图是该正三角形格点中的两个多边形(设格点多边形的面积为S,该多边形各边上的格点个数为m,内部的格点个数为n):
(1)根据图中提供的信息填表:
m | n-1 | s | |
多边形1 | 11 | ______ | 15 |
多边形2 | 8 | 1 | ______ |
… | … | … | … |
(2)则S与m、m-1之间的关系为______(用含m、n的代数式表示).
【答案】(1)3,10;(2)S=m+2(n-1).
【解析】
(1)根据题意和图形即可得出结果;
(2)由题意可知15=11+2×2,10=8+2×1,得出规律即可.
解:(1)填表如下:
m | n-1 | s | |
多边形1 | 11 | 2 | 15 |
多边形2 | 8 | 1 | 10 |
… | … | … | … |
故答案为:2,10;
(2)由题意可知15=11+2×2,10=8+2×1,
∴S=m+2(n-1);
故答案为:S=m+2(n-1).

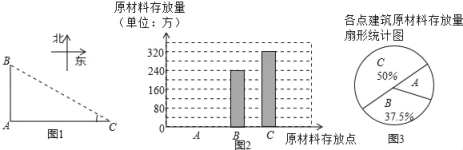
【题目】重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:
甲 | 乙 | 丙 | 丁 | |
∠C(单位:度) | 34 | 36 | 38 | 40 |
他们又调查了各点的建筑材料存放量,并绘制了下列尚不完整的统计如图、如图:
(1)求表中∠C度数的平均数![]() ;
;
(2)求A处的建筑原材料存放量,并将如图补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
【题目】某度假村拥有客房40间,该度假村在经营中发现每间客房日租金x(元)与每日租出的客房数(y)有如下关系:
x | 200 | 220 | 260 | 280 |
y | 40 | 35 | 25 | 20 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每日租出的客房数y(间)与每间客房的日租金x(元)之间的关系式.
(2)已知租出的每间客房每日需要清洁费80元,未租出的每间客房每日需要清洁费40元.含x(x≥200)的代数式填表:
租出的客房数 | ______ | 未租出的客房数 | ______ |
租出的每间客房的日收益 | ______ | 所有未租出的客房每日的清洁费 | ______ |
(3)若你是该度假村的老板,你会将每间客房的日租金定为多少元,才能使度假村获得最大日收益?最大日收益是多少元?