题目内容
【题目】边长为整数的直角三角形,若其两直角边边长是方程x2-(k+2)x+4k=0的两根,求k的值,并确定直角三角形三边之长。
【答案】当k=15时,三角形三边的长为:5,12,13.当k=12时,三角形三边的长为:6,8,10.
【解析】
根据方程的根为整数,得到根的判别式为平方数,然后进行讨论求出k值,得到三角形三边的长.
设直角边为a,b(a<b),则a+b=k+2,ab=4k,因为方程的根为整数,故△=(k+2)2-16k为完全平方数。
设(k+2)2-16k=n2∴k2-12k+4=n2∴(k-6)2-n2=32
∴(k+n-6)(k-n-6)=1×32=2×16=4×8
∵k+n-6>k-n-6
∴![]() ,
, ![]() ,
,![]() .
.
解得![]() (舍去),k2=15,k3=12
(舍去),k2=15,k3=12
当k2=15时,a+b=17,ab=60,
∴a=15, b=12, c=13;
当k=12时,a+b=14,ab=48,
∴a=6,b=8,c=10.
∴当k=15时,三角形三边的长为:5,12,13.
当k=12时,三角形三边的长为:6,8,10.

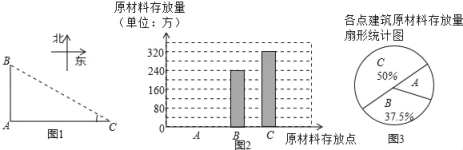
【题目】重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:
甲 | 乙 | 丙 | 丁 | |
∠C(单位:度) | 34 | 36 | 38 | 40 |
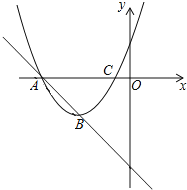
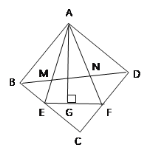
他们又调查了各点的建筑材料存放量,并绘制了下列尚不完整的统计如图、如图:
(1)求表中∠C度数的平均数![]() ;
;
(2)求A处的建筑原材料存放量,并将如图补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)