题目内容
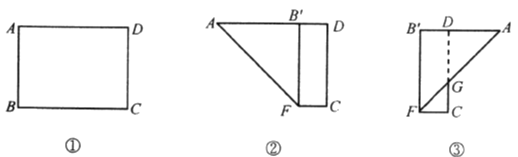
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 长为一边作
长为一边作![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() 、
、![]() 、
、![]() .
.
![]() 求证:
求证:![]()
![]() 当
当![]() ________时,
________时,![]() 是等边三角形,并说明理由.
是等边三角形,并说明理由.
![]() 当
当![]() 时,若
时,若![]() ,取
,取![]() 中点
中点![]() ,求
,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由直角三角形斜边上的中线性质即可得出结论;
(2)证明A、B、C、D共圆,E是圆心,由圆周定理得出∠BEC=2∠CAB,∠AED=2∠DBA,得出∠BEC+∠AED=2×60°=120°,求出∠DEC=60°,即可;
(3)同![]() 证出
证出![]() ,由直角三角形斜边上的中线性质即可得出结论.
,由直角三角形斜边上的中线性质即可得出结论.
![]() 证明:∵∠ACB=∠ADB=90°,
证明:∵∠ACB=∠ADB=90°,![]() 的中点,
的中点,
∴DE=![]() AB,CE=
AB,CE=![]() AB,
AB,
∴DE=CE;
![]() 当
当![]() 60°时,
60°时,![]() 是等边三角形,理由如下:
是等边三角形,理由如下:
∵∠ACB=∠ADB=90°,
∴A、B、C、D共圆,E是圆心,
∴∠BEC=2∠CAB,∠AED=2∠DBA,
∴∠CAB+∠DBA=60°,
∴∠BEC+∠AED=2×60°=120°,
∴∠DEC=60°,
∵DE=CE,
∴△DEC是等边三角形.
故答案为![]() ;
;
![]() 解:同
解:同![]() 得:
得:![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() .
.

练习册系列答案
相关题目