题目内容
【题目】如图，在⊙O中，AB为直径，C为⊙O上一点，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB=27°，求∠P的大小． 
【答案】解：连接OC，如图， ∵OA=OC，
∴∠OCA=∠A=27°，
∴∠POC=∠A+∠OCA=54°，
∵PC为切线，
∴OC⊥PC，
∴∠PCO=90°，
∴∠P=90°﹣∠POC=90°﹣54°=36°．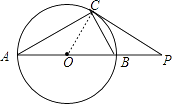
【解析】连接OC，如图，先利用等腰三角形的性质得到∠OCA=∠A=27°，再根据三角形外角性质得到∠POC=54°，接着根据切线的性质得到∠PCO=90°，然后利用互余计算∠P的度数．
【考点精析】通过灵活运用切线的性质定理，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
