题目内容
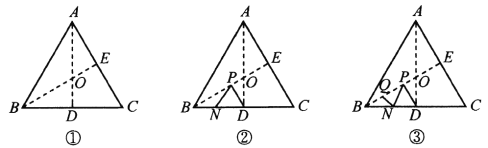
【题目】如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).

【答案】(1)证明见解析;(2)证明见解析;(3)②.
【解析】
(1)欲证明AE=CD,只要证明△ABE≌△CBD;
(2)由△ABE≌△CBD,推出BAE=∠BCD,由∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,又∠CNM=∠ABC,∠ABC=90°,可得∠NMC=90°;
(3)结论:②;作BK⊥AE于K,BJ⊥CD于J.理由角平分线的判定定理证明即可.
(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
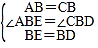 ,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°-∠BCD-∠CNM,∠ABC=180°-∠BAE-∠ANB,
又∠CNM=∠ABC,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
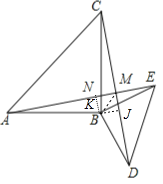
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴![]() AEBK=
AEBK=![]() CDBJ,
CDBJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△ABM≌△DBM,则AB=BD,显然可不能,故①错误.
故答案为②.

练习册系列答案
相关题目