题目内容
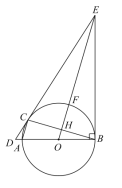
【题目】如图，已知
的直径AB垂直弦CD于点E，过C点作CG∥AD交AB延长线于点G，连结CO并延长交AD于点F，且CF⊥AD．
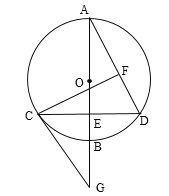
（1）求证：CG是⊙O的切线；
（2）若AB=4，求CD的长．
【答案】（1）见解析；（2）
【解析】
（1）已知点C在圆上，根据平行线的性质可得∠FCG=90°，即OC⊥CG；故CG是⊙O的切线．
（2）连接BD，先通过证明△BDE∽△OCE ，推出
，再由Rt△OCE中，通过三角函数的定义，可得CE=OE×cot30°，故代入OE=1可得CE的长．
（1）由题意知点C在圆上，
∵CF⊥AD，
∴∠AFC=90°
∵CG∥AD，
∴∠FCG=90°，
∴OC⊥CG．
∴CG是⊙O的切线；
（2）解：连接BD，如图，
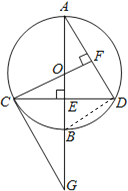
∵AB为⊙O的直径，
∴∠ADB=90°．
又∵∠AFO=90°，
∴∠ADB=∠AFO，∴CF∥BD．
∴△BDE∽△OCE．
∵AE⊥CD，且AE过圆心O，
∴CE=DE．
∴BE=OE．
∵AB=4，AB⊥CD
∴
，
又∵，
∴
∵AB⊥CD，
∴CD=2CE=．
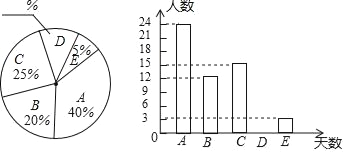
【题目】距离中考体考时间越来越近，年级想了解初三年级1512名学生周末在家体育锻炼的情况，在初三年级随机抽取了18名男生和18名女生，对他们周末在家的锻炼时间进行了调查，并收集得到了以下数据(单位：分钟)
男生：28，30，32，46，68，39，80，70，66，57，70，95，100，58，69，88，99，105
女生：36，48，78，99，56，62，35，109，29，88，88，69，73，55，90，98，69，72
统计数据，并制作了如下统计表：
时间 |
|
|
|
|
男生 | 2 |
|
| 4 |
女生 | 1 | 5 | 9 | 3 |
分析数据：两组数据的极差、平均数、中位数、众数如表所示
极差 | 平均数 | 中位数 | 方差 | ||
男生 | 77 | 66.7 |
| 70 | 617.3 |
女生 |
| 69.7 | 70.5 |
| 547.2 |
（1）请将上面的表格补充完整：
，
，
，
，
；
（2）已知该年级男女生人数差不多，根据调查的数据，估计初三年级周末在家锻炼的时间在90分钟以上(不包含90分钟)的同学约有多少人？
（3）体育老师看了表格数据后认为初三年级的女生周末锻炼做得比男生好，请你结合统计数据，写出两条支持体育老师观点的理由．
