ĚâÄżÄÚČÝ
ĄžĚâÄżĄżŇŃÖŞŁşČçÍźŁŹľă![]() ŁŹ
ŁŹ![]() ŁŹĎßśÎ
ŁŹĎßśÎ![]() Óë
Óë![]() ÖáĆ˝ĐĐŁŹÇŇ
ÖáĆ˝ĐĐŁŹÇŇ![]() ŁŹĹ×ÎďĎß
ŁŹĹ×ÎďĎß![]()
Ł¨1ŁŠľą![]() ĘąŁŹÇó¸ĂĹ×ÎďĎßÓë
ĘąŁŹÇó¸ĂĹ×ÎďĎßÓë![]() ÖáľÄ˝ťľă×řąęŁť
ÖáľÄ˝ťľă×řąęŁť
Ł¨2ŁŠľą![]() ĘąŁŹÇó
ĘąŁŹÇó![]() ľÄ×î´óÖľŁ¨ÓĂşŹ
ľÄ×î´óÖľŁ¨ÓĂşŹ![]() ľÄ´úĘýĘ˝ąíĘžŁŠŁť
ľÄ´úĘýĘ˝ąíĘžŁŠŁť
Ł¨3ŁŠľąĹ×ÎďĎß![]() žšýľă
žšýľă![]() ĘąŁŹ
ĘąŁŹ![]() ľÄ˝âÎöʽΪ__________ŁŹśĽľă×řąęÎŞ__________ŁŹľă
ľÄ˝âÎöʽΪ__________ŁŹśĽľă×řąęÎŞ__________ŁŹľă![]() __________Ł¨ĚĘÇĄąťňĄ°ˇńĄąŁŠÔÚ
__________Ł¨ĚĘÇĄąťňĄ°ˇńĄąŁŠÔÚ![]() ÉĎŁŽ
ÉĎŁŽ
ČôĎßśÎ![]() ŇÔĂżĂë2¸öľĽÎťł¤ľÄËŮśČĎňĎÂĆ˝ŇĆŁŹÉčĆ˝ŇĆľÄĘąźäÎŞ
ŇÔĂżĂë2¸öľĽÎťł¤ľÄËŮśČĎňĎÂĆ˝ŇĆŁŹÉčĆ˝ŇĆľÄĘąźäÎŞ![]() Ł¨Ă룊ŁŽ
Ł¨Ă룊ŁŽ
˘ŮČô![]() ÓëĎßśÎ
ÓëĎßśÎ![]() ×ÜÓĐšŤš˛ľăŁŹÇó
×ÜÓĐšŤš˛ľăŁŹÇó![]() ľÄČĄÖľˇśÎ§Łť
ľÄČĄÖľˇśÎ§Łť
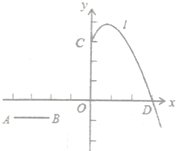
˘ÚČô![]() ÍŹĘąŇÔĂżĂë3¸öľĽÎťł¤ľÄËŮśČĎňĎÂĆ˝ŇĆŁŹ
ÍŹĘąŇÔĂżĂë3¸öľĽÎťł¤ľÄËŮśČĎňĎÂĆ˝ŇĆŁŹ![]() ÔÚ
ÔÚ![]() Öáź°ĆäÓҲŕľÄÍźĎóÓëÖąĎß
Öáź°ĆäÓҲŕľÄÍźĎóÓëÖąĎß![]() ×ÜÓĐÁ˝¸öšŤš˛ľăŁŹÖą˝ÓĐ´łö
×ÜÓĐÁ˝¸öšŤš˛ľăŁŹÖą˝ÓĐ´łö![]() ľÄČĄÖľˇśÎ§ŁŽ
ľÄČĄÖľˇśÎ§ŁŽ
Ąž´đ°¸ĄżŁ¨1ŁŠ![]() ŁŹ
ŁŹ![]() ŁťŁ¨2ŁŠľą
ŁťŁ¨2ŁŠľą![]() ĘąŁŹ
ĘąŁŹ ![]() ÓĐ×î´óÖľ0ŁŹľą
ÓĐ×î´óÖľ0ŁŹľą![]() ĘąŁŹ
ĘąŁŹ![]() ÓĐ×î´óÖľ
ÓĐ×î´óÖľ![]() ŁťŁ¨3ŁŠ
ŁťŁ¨3ŁŠ![]() ŁŹ
ŁŹ![]() ŁŹˇńŁť˘Ů
ŁŹˇńŁť˘Ů![]() Łť˘Ú
Łť˘Ú![]() ŁŽ
ŁŽ
Ąž˝âÎöĄż
Ł¨1ŁŠľąk=1ĘąŁŹ¸ĂĹ×ÎďĎß˝âÎöĘ˝y=x2-2x-3ŁŹy=0ĘąŁŹx2-2x-3=0ŁŹ˝âľĂx1=-1ŁŹx2=3ŁŹ¸ĂĹ×ÎďĎßÓëxÖáľÄ˝ťľă×řąęŁ¨-1ŁŹ0ŁŠŁŹŁ¨3ŁŹ0ŁŠŁť
Ł¨2ŁŠĹ×ÎďĎßy=kx2-2kx-3kľÄśÔłĆÖáÖąĎßx=![]() =1ŁŹľąkŁž0ĘąŁŹx=3ĘąŁŹyÓĐ×î´óÖľŁŹy×î´óÖľ=9k-6k-3k=0ŁŹľąkŁź0ĘąŁŹx=1ĘąŁŹyÓĐ×î´óÖľŁŹy×î´óÖľ=k-2k-3k=-4kŁť
=1ŁŹľąkŁž0ĘąŁŹx=3ĘąŁŹyÓĐ×î´óÖľŁŹy×î´óÖľ=9k-6k-3k=0ŁŹľąkŁź0ĘąŁŹx=1ĘąŁŹyÓĐ×î´óÖľŁŹy×î´óÖľ=k-2k-3k=-4kŁť
Ł¨3ŁŠľąĹ×ÎďĎßžšýľăCŁ¨0ŁŹ3ŁŠĘąŁŹĹ×ÎďĎ߾ĽâÎöʽΪy=-x2+2x+3ŁŹśĽľă×řąęŁ¨1ŁŹ4ŁŠŁŹAŁ¨-4ŁŹ-1ŁŠŁŹ˝Ťx=-2´úČëy=-x2+2x+3ŁŹy=-5ĄŮ-1ŁŹľăB˛ťÔÚlÉĎŁť
˘ŮÉčĆ˝ŇĆşóBŁ¨-2ŁŹ-1-2tŁŠŁŹAŁ¨-4ŁŹ-1-2tŁŠŁŹľąĹ×ÎďĎßžšýľăBĘąŁŹÓĐy=-5ŁŹľąĹ×ÎďĎßžšýľăAĘąŁŹÓĐy=-21ŁŹlÓëĎßśÎAB×ÜÓĐšŤš˛ľăŁŹÔň-21ĄÜ-1-2tĄÜ-5ŁŹ˝âľĂ2ĄÜtĄÜ10Łť
˘ÚĆ˝ŇĆšýłĚÖĐŁŹÉčCŁ¨0ŁŹ3-3tŁŠŁŹÔňĹ×ÎďĎ߾ĜĽľăŁ¨1ŁŹ4-3tŁŠŁŹÓÚĘÇ![]() ŁŹ˝âľĂ4ĄÜtŁź5ŁŽ
ŁŹ˝âľĂ4ĄÜtŁź5ŁŽ
˝âŁşŁ¨1ŁŠľą![]() ĘąŁŹĹ×ÎďĎß˝âÎöʽΪ
ĘąŁŹĹ×ÎďĎß˝âÎöʽΪ![]() ŁŹ
ŁŹ
ľą![]() ĘąŁŹ
ĘąŁŹ![]() ŁŹ˝âľĂ
ŁŹ˝âľĂ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
ËůŇÔ¸ĂĹ×ÎďĎßÓë![]() ÖáľÄ˝ťľăľÄ×řąęÎŞ
ÖáľÄ˝ťľăľÄ×řąęÎŞ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
Ł¨2ŁŠĹ×ÎďĎ߾ĜԳĆÖáÎŞÖąĎß![]() ŁŹ
ŁŹ
ľą![]() ĘąŁŹ
ĘąŁŹ![]() ĘąŁŹ
ĘąŁŹ![]() ŁŹ
ŁŹ![]() ÓĐ×î´óÖľ0ŁŹ
ÓĐ×î´óÖľ0ŁŹ
ľą![]() ĘąŁŹ
ĘąŁŹ![]() ĘąŁŹ
ĘąŁŹ![]() ŁŹ
ŁŹ![]() ÓĐ×î´óÖľ
ÓĐ×î´óÖľ![]() Łť
Łť
Ł¨3ŁŠ![]() ŁŹ
ŁŹ![]() ˇńŁť
ˇńŁť
˘ŮÉčľă![]() ľÄ×řąęÎŞ
ľÄ×řąęÎŞ![]() ŁŹľă
ŁŹľă![]() ľÄ×řąęÎŞ
ľÄ×řąęÎŞ![]() ŁŹ
ŁŹ
ľąĹ×ÎďĎß![]() žšýľă
žšýľă![]() ĘąŁŹÓĐ
ĘąŁŹÓĐ![]() ŁŹ
ŁŹ
ľąĹ×ÎďĎß![]() žšýľă
žšýľă![]() ĘąŁŹÓĐ
ĘąŁŹÓĐ![]() ŁŹ
ŁŹ
ľąĹ×ÎďĎß![]() ÓëĎßśÎ
ÓëĎßśÎ![]() ×ÜÓĐšŤš˛ľăĘąŁŹÓĐ
×ÜÓĐšŤš˛ľăĘąŁŹÓĐ![]() ŁŹ
ŁŹ
˝âľĂŁş![]() ŁŽ
ŁŽ
˘Ú![]() ŁŽ
ŁŽ