题目内容
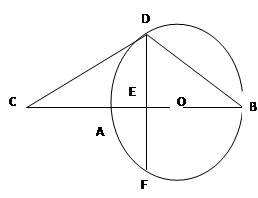
已知等腰△ABC中,AB=AC=5,BC=8,⊙O经过B、C两点,且AO=4,则⊙O的半径长是 .

解:如图,过A点作BC的垂直平分线,垂足为D,

∵AB=AC=5,BC=8,∴BD=4,
∴在Rt△ABD中,AD= AB2-BD2 =3,
当点O在A点上方时,OD=AO+AD=4+3=7,
在Rt△OBD中,半径OB=
当点O在A点下方时,O′D=AO′-AD=4-3=1,
在Rt△OBD中,半径O′B=
故答案为

∵AB=AC=5,BC=8,∴BD=4,
∴在Rt△ABD中,AD= AB2-BD2 =3,
当点O在A点上方时,OD=AO+AD=4+3=7,
在Rt△OBD中,半径OB=

当点O在A点下方时,O′D=AO′-AD=4-3=1,
在Rt△OBD中,半径O′B=

故答案为


练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 中,
中,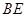 是它的角平分线,
是它的角平分线, ,
, 在
在 边上,
边上, 为直径的半圆
为直径的半圆 经过点
经过点 ,交
,交 于点
于点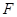 。
。
 是
是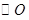 的切线;
的切线;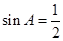 ,
,
 :2,求⊙O的半径及弦DF的长
:2,求⊙O的半径及弦DF的长