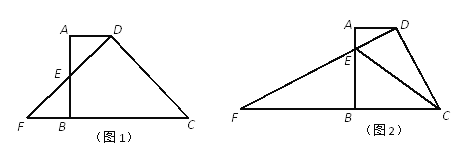Question

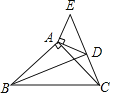
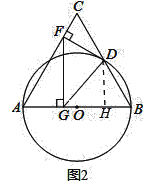
【题目】如图，已知等边△ABC，以AB为直径的圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连结GD．

（1）求证：DF是⊙O的切线；

（2）若AB＝12，求FG的长；

（3）在（2）问条件下，求点D到FG的距离．

Answer 1

【答案】（1）证明见解析；（2）；（3）．

【解析】

（1）连接OD，证明OD∥AC，易得OD⊥DF；

（2）先求出CD的长，再利用△CDF是30°的直角三角形可求出CF的长，同理可利用△FGA中∠A的三角函数可求得FG的长；

（3）过D作DH⊥AB于H，利用△BDH是30°的直角三角形可求出BH的长，同理可求得AG，然后根据GH=AB-AG-BH求得即可.

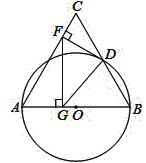
（1）证明：连结OD，如图1，

∵△ABC为等边三角形，

∴∠C＝∠A＝∠B＝60°．

而OD＝OB，

∴△ODB是等边三角形，∠ODB＝60°，

∴∠ODB＝∠C，

∴OD∥AC，

∵DF⊥AC，

∴OD⊥DF，

∴DF是⊙O的切线．

（2）解：∵OD∥AC，点O为AB的中点，

∴OD为△ABC的中位线．

∴BD＝CD＝6．

在Rt△CDF中，∠C＝60°，

∴∠CDF＝30°，

∴CF＝CD＝3．

∴AF＝AC﹣CF＝12﹣3＝9，

在Rt△AFG中，∵∠A＝60°，

∴FG＝AF×sinA＝9×＝．

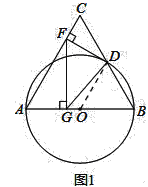
（3）解：如图2，过D作DH⊥AB于H．

∵FG⊥AB，DH⊥AB，

∴FG∥DH，

在Rt△BDH中，∠B＝60°，

∴∠BDH＝30°，

∴BH＝BD＝3，

在Rt△AFG中，∵∠AFG＝30°，

∴AG＝AF＝，

∵GH＝AB﹣AG﹣BH＝12﹣﹣3＝，

∴点D到FG的距离是．