Question

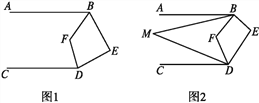
【题目】(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.

(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH＝90°, EF＝4.求GH的长.

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,∠FOH＝90°,EF＝4. 直接写出下列两题的答案：

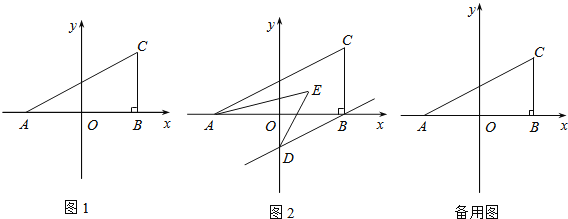
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；

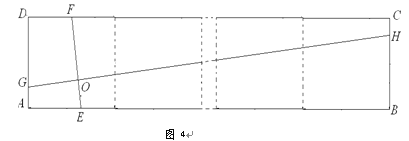
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

Answer 1

【答案】(1) 证明：如图1，

∵ 四边形ABCD为正方形，

∴ AB=BC,∠ABC=∠BCD=90°，

∴ ∠EAB+∠AEB=90°.

∵ ∠EOB=∠AOF＝90°,

∴ ∠FBC+∠AEB=90°，∴ ∠EAB=∠FBC，

∴ △ABE≌△BCF ， ∴ BE=CF． ………………3分

(2) 解：如图2,过点A作AM//GH交BC于M，

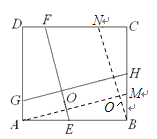
过点B作BN//EF交CD于N,AM与BN交于点O/，

则四边形AMHG和四边形BNFE均为平行四边形，

∴ EF=BN,GH=AM，

∵ ∠FOH＝90°, AM//GH，EF//BN, ∴ ∠NO/A=90°,

故由(1)得, △ABM≌△BCN， ∴ AM=BN，

∴ GH=EF=4． ………………6分

(3) ① 8．② 4n． ………………8分

【解析】（1）关键是证出∠CBF=∠BAE，可利用同角的余角相等得出，从而结合已知条件，利用SAS可证△ABE≌△BCF，于是BE=CF；

（2）过A作AM∥GH，交BC于M，过B作BN∥EF，交CD于N，AMBN交于点O′，利用平行四边形的判定，可知四边形AMHG和四边形BNFE是，那么AM=GH，BN=EF，由于∠EOH=90°，结合平行线的性质，可知∠AO′N=90°，那么此题就转化成（1），求△BCN≌△ABM即可；

（3）①若是两个正方形，则GH=2EF=8；②若是n个正方形，那么GH=n4=4n．