جâؤ؟ؤعبف
،¾جâؤ؟،؟شؤ¶ء²ؤءد£؛ ذ،أ÷شعر§د°¶´خ¸ùت½؛َ£¬·¢دضز»ذ©؛¬¸ù؛إµؤت½×س؟ةزشذ´³ةءيز»¸ِت½×سµؤئ½·½£¬بç£؛![]() £¬ةئسعث¼؟¼µؤذ،أ÷½ّذذءثزشدآج½ث÷£؛
£¬ةئسعث¼؟¼µؤذ،أ÷½ّذذءثزشدآج½ث÷£؛
ةè![]() £¨ئنضذ
£¨ئنضذ![]() ¾ùخھصûت£©£¬شٍسذ
¾ùخھصûت£©£¬شٍسذ ![]() £®
£®
،à![]() £®صâرùذ،أ÷¾حصزµ½ءثز»ضض°ر²؟·ض
£®صâرùذ،أ÷¾حصزµ½ءثز»ضض°ر²؟·ض![]() µؤت½×س»¯خھئ½·½ت½µؤ·½·¨£®
µؤت½×س»¯خھئ½·½ت½µؤ·½·¨£®
اëؤم·آصصذ،أ÷µؤ·½·¨ج½ث÷²¢½â¾ِدآءذختجâ£؛
£¨1£©µ±![]() ¾ùخھصصûتت±£¬بô
¾ùخھصصûتت±£¬بô![]() £¬سأ؛¬m،¢nµؤت½×س·ض±ً±يت¾
£¬سأ؛¬m،¢nµؤت½×س·ض±ً±يت¾![]() £¬µأ
£¬µأ ![]() £½،، ،،£¬
£½،، ،،£¬![]() £½،، ،،£»
£½،، ،،£»
£¨2£©ہûسأثùج½ث÷µؤ½لآغ£¬صزز»×éصصûت![]() £¬جî؟ص£؛ £«،، ،،
£¬جî؟ص£؛ £«،، ،،![]() £½(،، ،،£«،، ،،
£½(،، ،،£«،، ،،![]() )2£»
)2£»
£¨3£©بô![]() £¬از
£¬از![]() ¾ùخھصصûت£¬اَ
¾ùخھصصûت£¬اَ![]() µؤضµ£®
µؤضµ£®
،¾´ً°¸،؟£¨1£©![]() £»
£»![]() £»£¨2£©4£¬2£¬1£¬1£¨´ً°¸²»خ¨ز»£©£»£¨3£©
£»£¨2£©4£¬2£¬1£¬1£¨´ً°¸²»خ¨ز»£©£»£¨3£©![]() £½7»ٍ13
£½7»ٍ13
،¾½âخِ،؟·ضخِ£؛£¨1£©سةa+b![]() =(m+n
=(m+n![]() )2£¬ص¹؟ھ±ب½ددµت؟ةµأ´ً°¸£»
)2£¬ص¹؟ھ±ب½ددµت؟ةµأ´ً°¸£»
£¨2£©ب،m=1£¬n=1£¬؟ةµأa؛حbµؤضµ£¬؟ةµأ´ً°¸£»
£¨3£©سةجâزâµأm؛حnµؤ·½³ج£¬½â·½³ج؟ةµأm؛حn£¬؟ةµأaضµ£®
دê½â£؛£¨1£©،كa+b![]() =(m+n
=(m+n![]() )2£¬
)2£¬
،àa+b![]() =m2+3n2+2mn
=m2+3n2+2mn![]() £¬
£¬
،àa=m2+3n2£¬b=2mn£®
¹ت´ً°¸خھ£؛m2+3n2£¬2mn£®
£¨2£©ةèm=1£¬n=1£¬
،àa=m2+3n2=4£¬b=2mn=2£®
¹ت´ً°¸خھ4،¢2،¢1،¢1£®
£¨3£©سةجâز⣬µأ£؛
a=m2+3n2£¬b=2mn
،ك4=2mn£¬ازm،¢nخھصصûت£¬
،àm=2£¬n=1»ٍصكm=1£¬n=2£¬
،àa=22+3،ء12=7£¬»ٍa=12+3،ء22=13£®
µم¾¦£؛±¾جâض÷زھ؟¼²é¶´خ¸ùت½µؤ»ى؛دشثثم£¬حêب«ئ½·½¹«ت½£¬½âجâµؤ¹ط¼üشعسعتىء·شثثمحêب«ئ½·½¹«ت½؛ح¶´خ¸ùت½µؤشثثم·¨شٍ£®
،¾جâذح،؟½â´ًجâ
،¾½لتّ،؟
28
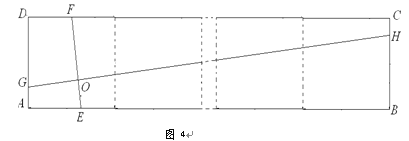
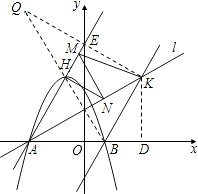
،¾جâؤ؟،؟بçح¼1£¬زرضھµمA£¨a£¬0£©£¬B£¨0£¬b£©£¬ازa،¢bآْ×م![]() £¬
£¬
،ُABCDµؤ±كADسëyضل½»سعµمE£¬ازEخھADضذµم£¬ث«اْدك![]() ¾¹C،¢Dء½µم£®
¾¹C،¢Dء½µم£®
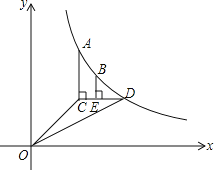
£¨1£©بôµمDµم×ف×ّ±êخھt£¬شٍCµم×ف×ّ±êخھ £¨؛¬tµؤ´ْتت½±يت¾£©£¬kµؤضµخھ £»
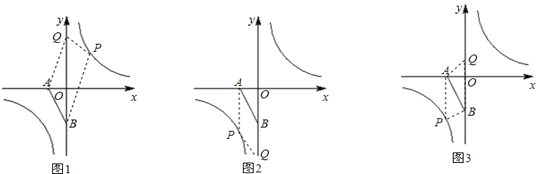
£¨2£©µمPشعث«اْدك![]() ةد£¬µمQشعyضلةد£¬بôزشµمA،¢B،¢P،¢Qخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخ£¬تشاَآْ×مزھاَµؤثùسذµمP،¢Qµؤ×ّ±ê£»
ةد£¬µمQشعyضلةد£¬بôزشµمA،¢B،¢P،¢Qخھ¶¥µمµؤثؤ±كذختائ½ذذثؤ±كذخ£¬تشاَآْ×مزھاَµؤثùسذµمP،¢Qµؤ×ّ±ê£»
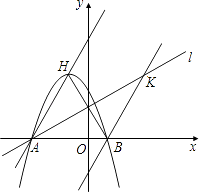
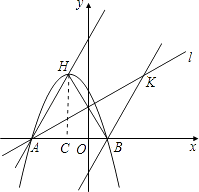
£¨3£©زشدك¶خABخھ¶ش½ادك×÷ص·½ذخAFBH£¨بçح¼3£©£¬µمTتا±كAFةدز»¶¯µم£¬MتاHTµؤضذµم£¬MN،حHT£¬½»ABسعN£¬ء¬½سFN£¬µ±TشعAFةدشث¶¯ت±£¬تشإذ¶د،دATHسë،دAFNض®¼نµؤتء؟¹طدµ£¬²¢ثµأ÷ہيسة،£


،¾´ً°¸،؟£¨1£©t-3£¬6£»£¨2£©![]() £¨1£¬6£©£¬
£¨1£¬6£©£¬![]() £¨0£¬9£©£»£»
£¨0£¬9£©£»£»![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬-9£©£»
£¨0£¬-9£©£»![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬3£©£»£¨3£©،دATH+،دAFN=135،م£®
£¨0£¬3£©£»£¨3£©،دATH+،دAFN=135،م£®
،¾½âخِ،؟·ضخِ£؛£¨1£©دب¸ù¾ف·ا¸؛تµؤذشضتاَ³ِa،¢bµؤضµ£¬¹ت؟ةµأ³ِA،¢Bء½µمµؤ×ّ±ê£¬ةèD£¨1£¬t£©£¬سةDC،خAB£¬؟ةضھC£¨2£¬t-2£©£¬شظ¸ù¾ف·´±بہ؛¯تµؤذشضتاَ³ِtµؤضµ¼´؟ة£»
£¨2£©سة£¨1£©ضھk=4؟ةضھ·´±بہ؛¯تµؤ½âخِت½خھy=![]() £¬شظسةµمPشعث«اْدكy=
£¬شظسةµمPشعث«اْدكy=![]() ةد£¬µمQشعyضلةد£¬ةèQ£¨0£¬y£©£¬P£¨x£¬
ةد£¬µمQشعyضلةد£¬ةèQ£¨0£¬y£©£¬P£¨x£¬![]() £©£¬شظ·ضزشABخھ±ك؛حزشABخھ¶ش½ادكء½ضضاé؟ِاَ³ِxµؤضµ£¬¹ت؟ةµأ³ِP،¢Qµؤ×ّ±ê£»
£©£¬شظ·ضزشABخھ±ك؛حزشABخھ¶ش½ادكء½ضضاé؟ِاَ³ِxµؤضµ£¬¹ت؟ةµأ³ِP،¢Qµؤ×ّ±ê£»
£¨3£©ء¬NH،¢NT،¢NF£¬ز×ض¤NF=NH=NT£¬¹ت،دNTF=،دNFT=،دAHN£¬،دTNH=،دTAH=90،م£¬MN=![]() HTسة´ث¼´؟ةµأ³ِ½لآغ£®
HTسة´ث¼´؟ةµأ³ِ½لآغ£®
دê½â£؛£¨1£©،ك![]() £¬از،àa+1£½0,a+b+4£½0£¬½âµأ£؛a£½1£»b£½3£¬
£¬از،àa+1£½0,a+b+4£½0£¬½âµأ£؛a£½1£»b£½3£¬
،àA£¨-1£¬0£©£¬B£¨0£¬-3£©£¬،كEخھADضذµم£¬،àxD=1£¬ةèD£¨1£¬t£©£¬
سض،كDC،خAB£¬،àC£¨2£¬t-3£©£¬،àt=2t-6£¬،àt=6£¬،àk=6£»
£¨2£©،كسة£¨1£©ضھk=6£¬
،à·´±بہ؛¯تµؤ½âخِت½خھ![]() £¬،كµمPشعث«اْدك
£¬،كµمPشعث«اْدك![]() ةد£¬µمQشعyضلةد£¬
ةد£¬µمQشعyضلةد£¬
،àةèQ£¨0£¬y£©£¬P£¨![]() £¬
£¬
¢ظABخھ±كت±£؛
بçح¼1ثùت¾£؛ بôABPQخھئ½ذذثؤ±كذخ£¬شٍ![]() £¬
£¬
½âµأx=1£¬´ثت±![]() £¨1£¬6£©£¬
£¨1£¬6£©£¬![]() £¨0£¬9£©£»
£¨0£¬9£©£»
بçح¼2ثùت¾£»بôABQPخھئ½ذذثؤ±كذخ£¬شٍ![]() £¬
£¬
½âµأx=-1£¬´ثت±![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬-9£©£» /p>
£¨0£¬-9£©£» /p>
¢عبçح¼3ثùت¾£»µ±ABخھ¶ش½ادكت±£؛AP=BQ£¬ازAP،خBQ£»
،à![]() £¬½âµأx=-1£¬،à
£¬½âµأx=-1£¬،à![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬3£©£»
£¨0£¬3£©£»
¹ت![]() £¨1£¬6£©£¬
£¨1£¬6£©£¬![]() £¨0£¬9£©£»£»
£¨0£¬9£©£»£»![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬-9£©£»
£¨0£¬-9£©£»![]() £¨-1£¬-6£©£¬
£¨-1£¬-6£©£¬![]() £¨0£¬3£©£»
£¨0£¬3£©£»
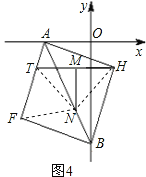
£¨3£©ء¬NH،¢NT،¢NF£¬،كMNتادك¶خHTµؤ´¹ض±ئ½·ضدك£¬
،àNT=NH£¬،كثؤ±كذخAFBHتاص·½ذخ£¬،à،دABF=،دABH£¬
شع،÷BFNسë،÷BHNضذ£¬،كBF£½BH£¬،دABF£½،دABH£¬BN£½BN£¬
،à،÷BFN،ص،÷BHN£¬،àNF=NH=NT£¬،à،دNTF=،دNFT=،دAHN£¬
ثؤ±كذخATNHضذ£¬،دATN+،دNTF=180،م£¬
¶ّ،دNTF=،دNFT=،دAHN£¬
ثùزش£¬،دATN+،دAHN=180،م£¬
ثùزش£¬ثؤ±كذخATNHؤع½ا؛حخھ360،م£¬
ثùزش،دTNH=360،م-180،م-90،م=90،م£®
،دATH+،دAFN=135،م£®