题目内容
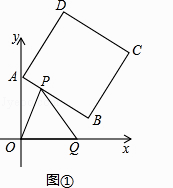
【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD. 
求证:
(1)△APB≌△DPC;
(2)∠BAP=2∠PAC.
【答案】
(1))解:∵四边形ABCD是正方形,∴∠ABC=∠DCB=90°.
∵PB=PC,∴∠PBC=∠PCB.
∴∠ABC﹣∠PBC=∠DCB﹣∠PCB,即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
(2))解:证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,∴AP=DP.
又∵AP=AB=AD,∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP﹣∠DAC=15°.
∴∠BAP=∠BAC﹣∠PAC=30°.
∴∠BAP=2∠PAC.
【解析】(1)AP=AB,PB=PC,∴∠ABC﹣∠PBC=∠DCB﹣∠PCB,即∠ABP=∠DCP,因此可证得两三角形全等.(2)有(1)∠CAD=45°,△PAD为等边三角形,可求得∠BAP=30°∠PAC=∠PAD﹣∠CAD=15°,因此可证的结论.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
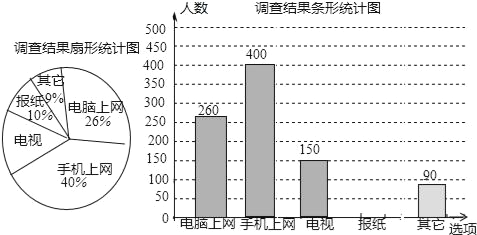
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图. 上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a=;b=;
(2)补全频数分布直方图; 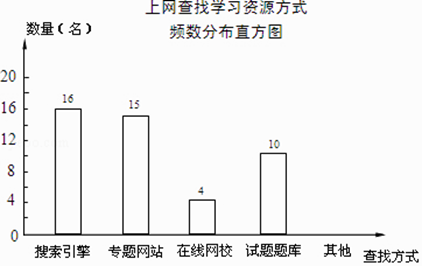
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?