Question

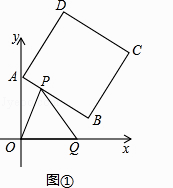
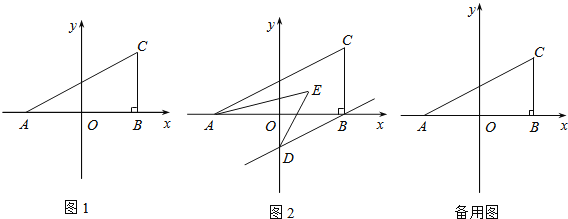
【题目】如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足，过C作CB⊥x轴于B，

（1）求a，b的值；

（2）在y轴上是否存在点P，使得△ABC和△OCP的面积相等，求出P点坐标；

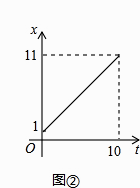
（3）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，

①求：∠CAB＋∠ODB的度数；

②求：∠AED的度数.

Answer 1

【答案】（1）a＝﹣2，b＝2，（2）P点坐标为（0，4）或（0，﹣4）；（3）①90°；②45°.

【解析】

试题（1）由非负数的性质得到a＋2＝0，b－2＝0，从而得到a、b的值；

（2）由A（﹣2，0），C（2，2），S△OPC =S△ABC＝4，可以得到OP的长，从而得到P的坐标；

（3）①由平行线的性质和直角三角形的两锐角互余即可得到结论；

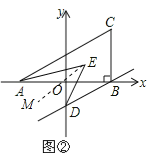
②过E作EM∥AC， 由平行线的性质和角平分线的性质即可得出结论．

试题解析：解：（1）∵，且， ∴a＋2＝0，b－2＝0，∴a＝﹣2，b＝2；

（2）由（1）知A（﹣2，0），C（2，2）， ∴S△ABC＝4，∴S△OPC=|OP |×2＝4×2÷2＝4， ∴OP=4，∴P点坐标为（0，4）或（0，﹣4）；

（3）①∵BD∥AC，∴∠CAB＝∠OBD．∵∠ODB＋∠OBD＝90°，∴∠CAB＋∠ODB＝90°；

②过E作EM∥AC．∵BD∥AC，∴BD∥AC∥EM．∵AE，DE分别平分∠CAB，∠ODB，∴∠CAE＝∠CAB＝∠AEM，∠EDB＝∠ODB＝∠DEM，∴∠AED＝∠AEM＋∠DEM＝（∠CAB＋∠ODB）＝45°．