题目内容
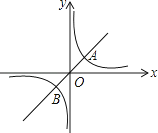
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0, ![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
【答案】
(1)解:如图1,过C作CE⊥OA于E,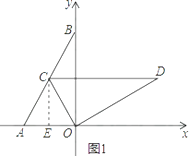
∵点A,点B坐标分别为(﹣1,0),(0, ![]() ),
),
∴OA=1,OB= ![]() ,
,
∵△AOB绕点O顺时针旋转60°得到△COD,
∴∠AOC=∠BOD=60°,AO=OC=1,
∴OE= ![]() OC=
OC= ![]() ,CE=
,CE= ![]() OC=
OC= ![]() ,
,
∴C(﹣ ![]() ,
, ![]() )
)
(2)解:△AOB绕点O顺时针旋转60°所扫过的面积= ![]() +
+ ![]() +
+ ![]() ×
× ![]() =
= ![]() π+
π+ ![]()
(3)解:如图2,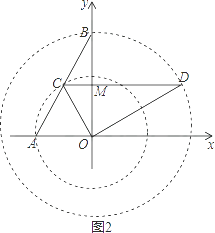
线段AB绕点O顺时针旋转60°所扫过的面积═( ![]() ﹣1×
﹣1× ![]() )+(
)+(![]()
![]() )+
)+![]() (
( ![]() ﹣
﹣ ![]() )=
)= ![]() .
.
【解析】(1)根据题意可作辅助线,过C作CE⊥OA于E,由旋转的性质可得∠AOC=∠BOD=60°,AO=OC=1,再由直角三角形中,30度角所对的直角边等于斜边的一半可求得OE的长,在直角三角形CEO中,用锐角三角函数可求CE的长,根据点C在第二象限可写出点C的坐标。
(2)由题意结合图形可得,△AOB绕点O顺时针旋转60°所扫过的面积=扇形AOC的面积+扇形BOD的面积+三角形BOC的面积。
(3)由题意结合图形可得,线段AB绕点O顺时针旋转60°所扫过的面积═扇形AOC的面积-三角形AOC的面积+扇形BOD的面积-三角形DOM的面积+三角形BCM的面积。扇形面积=n![]()
![]()
![]() 360.
360.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目