题目内容
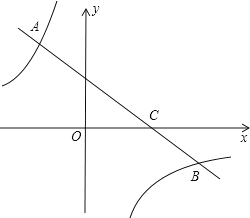
【题目】如图,反比例函数![]() (k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.
(k>0)与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.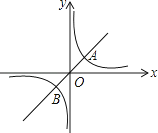
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与函数![]() (k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
(k>0)的图象交于C(x1 , y1),D(x2 , y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
【答案】
(1)
解:据题意得:点A(1,k)与点B(﹣k,﹣1)关于原点对称,
∴k=1,
∴A(1,1),B(﹣1,﹣1),
∴反比例函数和正比例函数的解析式分别为![]() ,y=x;
,y=x;
(2)
解:∵一次函数y=x+b的图象过点(x1,y1)、(x2,y2),
∴![]() ,
,
②﹣①得,y2﹣y1=x2﹣x1,
∵|x1﹣x2||y1﹣y2|=5,
∴|x1﹣x2|=|y1﹣y2|=![]() ,
,
由 得x2+bx﹣1=0,
得x2+bx﹣1=0,
解得,x1=![]() ,x2=
,x2=![]() ,
,
∴|x1﹣x2|=|![]() ﹣
﹣![]() |=|
|=|![]() |=
|=![]() ,
,
解得b=±1.
【解析】(1)首先根据点A与点B关于原点对称,可以求出k的值,将点A分别代入反比例函数与正比例函数的解析式,即可得解.
(2)分别把点(x1 , y1)、(x2 , y2)代入一次函数y=x+b,再把两式相减,根据|x1﹣x2||y1﹣y2|=5得出|x1﹣x2|=|y1﹣y2|=![]() , 然后通过联立方程求得x1、x2的值,代入即可求得b的值.
, 然后通过联立方程求得x1、x2的值,代入即可求得b的值.

练习册系列答案
相关题目