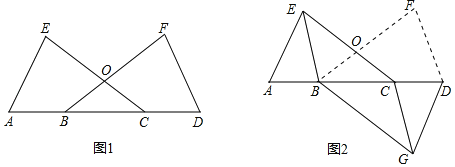题目内容
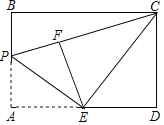
【题目】如图1,在矩形ABCD中,E是CD上一点,动点P从点A出发沿折线AE→EC→CB运动到点B时停止,动点Q从点A沿AB运动到点B时停止,它们的速度均为每秒1cm.如果点P、Q同时从点A处开始运动,设运动时间为x(s),△APQ的面积为ycm2,已知y与x的函数图象如图2所示,以下结论:①AB=5cm;②cos∠AED=![]() ;③当0≤x≤5时,y=
;③当0≤x≤5时,y=![]() ;④当x=6时,△APQ是等腰三角形;⑤当7≤x≤11时,y=
;④当x=6时,△APQ是等腰三角形;⑤当7≤x≤11时,y=![]() .其中正确的有( )
.其中正确的有( )
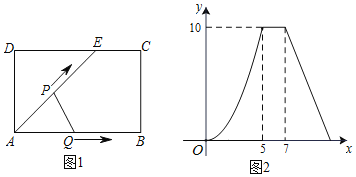
A.2个B.3个C.4个D.5个
【答案】B
【解析】
根据图中相关信息即可判断出正确答案.
解:图2知:当![]() 时y恒为10,
时y恒为10,
∴当![]() 时,点Q运动恰好到点B停止,且当
时,点Q运动恰好到点B停止,且当![]() 时点P必在EC上,
时点P必在EC上,
![]() 故①正确;
故①正确;
∵当![]() 时点P必在EC上,且当
时点P必在EC上,且当![]() 时,y逐渐减小,
时,y逐渐减小,
∴当![]() 时,点Q在点B处,点P在点C处,此时
时,点Q在点B处,点P在点C处,此时![]()
![]()
设![]() 则
则![]()
![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
解得:![]()
![]()
![]() 故②正确;
故②正确;
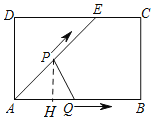
当![]() 时,由
时,由![]() 知点P在AE上,过点P作
知点P在AE上,过点P作![]() 如图:
如图:
![]()
![]()
![]()
![]()
![]() 故③正确;
故③正确;
当![]() 时,
时,![]()
![]()
![]() 不是等腰三角形,故④不正确;
不是等腰三角形,故④不正确;
当![]() 时,点P在BC上,点Q和点B重合,
时,点P在BC上,点Q和点B重合,![]()
故⑤ 不正确;
故选B.

【题目】已知函数y=y1+y2,其中y1与x成反比例,y2与x﹣2成正比例,函数的自变量x的取值范围是x≥![]() ,且当x=1或x=4时,y的值均为
,且当x=1或x=4时,y的值均为![]() .
.
请对该函数及其图象进行如下探究:
(1)解析式探究:根据给定的条件,可以确定出该函数的解析式为: .
(2)函数图象探究:
①根据解析式,补全下表:
x |
| 1 |
| 2 |
| 3 | 4 | 6 | 8 | … |
y |
|
|
|
|
|
|
| … |
②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.

(3)结合画出的函数图象,解决问题:
①当x=![]() ,
,![]() ,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
,8时,函数值分别为y1,y2,y3,则y1,y2,y3的大小关系为: ;(用“<”或“=”表示)
②若直线y=k与该函数图象有两个交点,则k的取值范围是 ,此时,x的取值范围是 .