题目内容
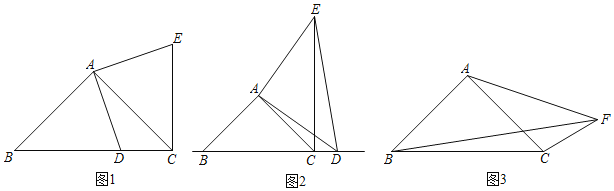
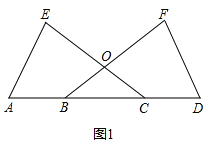
【题目】如图1,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
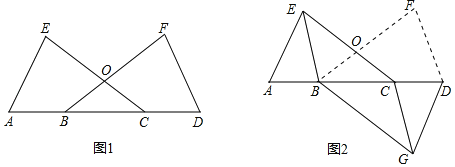
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)直接利用等腰三角形的性质结合全等三角形的判定与性质得出即可;
(2)利用翻折变换的性质得出∠DBG=∠DBF,再利用平行线的判定方法得出CE∥BG,进而求出四边形BGCE是平行四边形
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
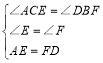 ,
,
∴△ACE≌△DBF(AAS);
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目