题目内容
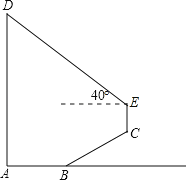
【题目】如图，为了测量建筑物AD的高度，小亮从建筑物正前方10米处的点B出发，沿坡度i＝1：
的斜坡BC前进6米到达点C，在点C处放置测角仪，测得建筑物顶部D的仰角为40°，测角仪CE的高为1.3米，A、B、C、D、E在同一平面内，且建筑物和测角仪都与地面垂直求建筑物AD的高度．（结果精确到0.1米参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，≈1.73）
【答案】建筑物AD的高度约为17.1米．
【解析】
延长EC交AB于F，作EM⊥AD于M，根据坡比的定义求出
,根据正切的定义求出
,计算即可.
解：延长EC交AB于F，作EM⊥AD于M，如下图所示：
则四边形MAFE为矩形，
∴MA＝EF，ME＝AF，
∵斜坡BC的坡度
，BC＝6，
∴CF＝3，
，
∴
，
在
中，
，
∴
，
∴
，
答：建筑物AD的高度约为17.1米．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
