Question

【题目】等腰三角形一腰上的高与另一腰的夹角为40°，则等腰三角形底角的度数是________________°．

Answer 1

【答案】65或25

【解析】

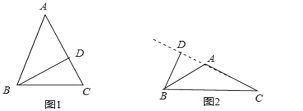
在等腰△ABC中，AB＝AC，BD为腰AC上的高，∠ABD＝40°，讨论：当BD在△ABC内部时，如图1，先计算出∠BAD＝50°，再根据等腰三角形的性质和三角形内角和可计算出∠ACB；当BD在△ABC外部时，如图2，先计算出∠BAD＝50°，再根据等腰三角形的性质和三角形外角性质可计算出∠ACB．

在等腰△ABC中，AB＝AC，BD为腰AC上的高，∠ABD＝40°，

当BD在△ABC内部时，如图1，

∵BD为高，

∴∠ADB＝90°，

∴∠BAD＝90°40°＝50°，

∵AB＝AC，

∴∠ABC＝∠ACB＝（180°50°）＝65°；

当BD在△ABC外部时，如图2，

∵BD为高，

∴∠ADB＝90°，

∴∠BAD＝90°40°＝50°，

∵AB＝AC，

∴∠ABC＝∠ACB，

而∠BAD＝∠ABC＋∠ACB，

∴∠ACB＝∠BAD＝25°，

综上所述，这个等腰三角形底角的度数为65°或25°．

故填：65或25.