Question

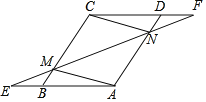
【题目】如图,直线AB和直线BC相交于点B,连接AC,点D. E. H分别在AB、AC、BC上,连接DE、DH,F是DH上一点,已知∠1+∠3=180°，

(1)求证：∠CEF=∠EAD；

(2)若DH平分∠BDE,∠2=α,求∠3的度数.(用α表示).

Answer 1

【答案】（1）证明见解析；（2）90+ α.

【解析】

（1）根据平行线的判定和性质解答即可；

（2）根据平行线的性质解答即可．

(1)∵∠3+∠DFE=180°,∠1+∠3=180°，

∴∠DFE=∠1，

∴AB∥EF，

∴∠CEF=∠EAD；

(2)∵AB∥EF，

∴∠2+∠BDE=180°

又∵∠2=α

∴∠BDE=180°α

又∵DH平分∠BDE

∴∠1=∠BDE= (180°α)

∴∠3=180° (180°α)=90+ α