ЬтФПФкШн
ЁОЬтФПЁПЮЪЬтБГОАЃКЮвУЧбЇЯАСЫећЪНЕФГЫЗЈЃЌСНИіЖрЯюЪНЯрГЫЃЌЮвУЧПЩвддЫгУЗЈдђЃЌНЋЦфеЙПЊЃЌР§ШчЃК![]() ЃЌЖјНЋЕШКХЕФзѓгвСНБпЛЅЛЛЃЌЮвУЧЕУЕНСЫ
ЃЌЖјНЋЕШКХЕФзѓгвСНБпЛЅЛЛЃЌЮвУЧЕУЕНСЫ![]() ЃЌЕШКХЕФзѓБпЪЧвЛИіЖрЯюЪНЃЌЖјгвБпЪЧМИИіећЪНЯрГЫЕФаЮЪНЃЌЮвУЧЙцЖЈНЋвЛИіЖрЯюЪНаДГЩМИИіећЪНЯрГЫЕФаЮЪНЃЌетжждЫЫуГЦжЎЮЊЁАвђЪНЗжНтЁБ
ЃЌЕШКХЕФзѓБпЪЧвЛИіЖрЯюЪНЃЌЖјгвБпЪЧМИИіећЪНЯрГЫЕФаЮЪНЃЌЮвУЧЙцЖЈНЋвЛИіЖрЯюЪНаДГЩМИИіећЪНЯрГЫЕФаЮЪНЃЌетжждЫЫуГЦжЎЮЊЁАвђЪНЗжНтЁБ
ЮЪЬтЬсГіЃК
ШчКЮНЋ![]() НјаавђЪНЗжНтФиЃП
НјаавђЪНЗжНтФиЃП
ЮЪЬтЬНОПЃК
Ъ§аЮНсКЯЪЧНтОіЪ§бЇЮЪЬтЕФвЛжжживЊЕФЫМЯыЗНЗЈЃЌНшжњетжжЗНЗЈПЩНЋГщЯѓЕФЪ§бЇжЊЪЖБфЕУжБЙлЦ№РДВЂЧвОпгаПЩВйзїадЃЌДгЖјПЩвдАяжњЮвУЧПьЫйНтЬт.ГѕжаЪ§бЇРяЕФвЛаЉДњЪ§ЙЋЪНЃЌКмЖрЖМПЩвдЭЈЙ§БэЪОМИКЮЭМаЮУцЛ§ЕФЗНЗЈНјаажБЙлЭЦЕМКЭНтЪЭ
Р§ШчЃКЮвУЧПЩвдЭЈЙ§БэЪОМИКЮЭМаЮУцЛ§ЕФЗНЗЈРДПьЫйЕФЖдЖрЯюЪН![]() НјаавђЪНЗжНт.
НјаавђЪНЗжНт.
ШчЭМЫљЪОБпГЄЮЊ![]() ЕФДѓе§ЗНаЮЪЧгЩ1ИіБпГЄЮЊ
ЕФДѓе§ЗНаЮЪЧгЩ1ИіБпГЄЮЊ![]() ЕФе§ЗНаЮЃЌ2ИіБпГЄЮЊ
ЕФе§ЗНаЮЃЌ2ИіБпГЄЮЊ![]() ЕФГЄЗНаЮЃЌ1ИіБпГЄЮЊ
ЕФГЄЗНаЮЃЌ1ИіБпГЄЮЊ![]() ЕФе§ЗНаЮЃЌ
ЕФе§ЗНаЮЃЌ![]() зщГЩЃЌЮвУЧПЩвдгУСНжжЗНЗЈБэЪОДѓе§ЗНаЮЕФУцЛ§ЃЌетИіЭМаЮЕФУцЛ§ПЩвдБэЪОГЩЃК
зщГЩЃЌЮвУЧПЩвдгУСНжжЗНЗЈБэЪОДѓе§ЗНаЮЕФУцЛ§ЃЌетИіЭМаЮЕФУцЛ§ПЩвдБэЪОГЩЃК![]() Лђ
Лђ![]()
Ёр![]()
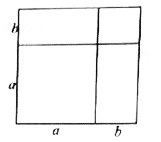
ЮвУЧНЋЕШКХзѓБпЕФЖрЯюЪНаДГЩСЫгвБпСНИіећЪНЯрГЫЕФаЮЪНЃЌДгЖјГЩЙІЕФЖдЖрЯюЪН![]() НјааСЫвђЪНЗжНт
НјааСЫвђЪНЗжНт
ЧыФуРрБШЩЯЪіЗНЗЈЃЌРћгУЭМаЮЕФМИКЮвтвхЖдЖрЯюЪН![]() НјаавђЪНЗжНтЃЈвЊЧѓздМКЙЙЭМВЂаДГіЭЦжЄЙ§ГЬЃЉ
НјаавђЪНЗжНтЃЈвЊЧѓздМКЙЙЭМВЂаДГіЭЦжЄЙ§ГЬЃЉ
ЮЪЬтЭиеЙЃК
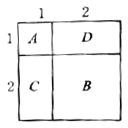
ШчКЮРћгУЭМаЮМИКЮвтвхЕФЗНЗЈЭЦЕМЃК![]() ЃПШчЭМЃЌ
ЃПШчЭМЃЌ![]() БэЪО1Иі
БэЪО1Иі![]() ЕФе§ЗНаЮЃЌМД
ЕФе§ЗНаЮЃЌМД![]() ЃЌ
ЃЌ![]() БэЪО1Иі
БэЪО1Иі![]() ЕФе§ЗНаЮЃЌ
ЕФе§ЗНаЮЃЌ![]() гы
гы![]() ЧЁКУПЩвдЦДГЩ1Иі
ЧЁКУПЩвдЦДГЩ1Иі![]() ЕФе§ЗНаЮЃЌвђДЫЃК
ЕФе§ЗНаЮЃЌвђДЫЃК![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ОЭПЩвдБэЪО2Иі
ОЭПЩвдБэЪО2Иі![]() ЕФе§ЗНаЮЃЌМД
ЕФе§ЗНаЮЃЌМД![]() ЃЌЖј
ЃЌЖј![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЧЁКУПЩвдЦДГЩвЛИі
ЧЁКУПЩвдЦДГЩвЛИі![]() ЕФДѓе§ЗНаЮ.гЩДЫПЩЕУЃК
ЕФДѓе§ЗНаЮ.гЩДЫПЩЕУЃК![]()
ГЂЪдНтОіЃК
ЧыФуРрБШЩЯЪіЭЦЕМЙ§ГЬЃЌРћгУЭМаЮМИКЮвтвхЗНЗЈЭЦЕМГі![]() ЕФжЕ.
ЕФжЕ.
ЃЈвЊЧѓздМКЙЙдьЭМаЮВЂаДГіЭЦжЄЙ§ГЬЃЉ.
НтЃК
ЙщФЩВТЯыЃК![]() _________________.
_________________.
ЁОД№АИЁП![]() ЃЛ
ЃЛ ![]() ЃЛ
ЃЛ![]()
ЁОНтЮіЁП
ЮЪЬтЬНОПЃК
РћгУе§ЗНаЮжНЦЌ3еХЃЌГЄЗНаЮжНЦЌ3еХЃЌМДПЩЦДГЩвЛИіГЄЗНаЮЃЌвРОнЭМаЮМДПЩНЋЖрЯюЪН![]() аДГЩСНИіећЪНГЫЛ§ЕФаЮЪНЃЎ
аДГЩСНИіећЪНГЫЛ§ЕФаЮЪНЃЎ
ГЂЪдНтОіЃК
ИљОнЙцТЩПЩвдРћгУЯрЭЌЕФЗНЗЈНјааЬНОПЭЦжЄЃЌгЩДЫЬНОП![]() ПЯЖЈЙЙГЩДѓе§ЗНаЮга9ИіЛљБОЭМаЮЃЈ3Иіе§ЗНаЮ6ИіГЄЗНаЮЃЉзщГЩЃЌШчЭМЫљЪОПЩвдЭЦжЄЃЎ
ПЯЖЈЙЙГЩДѓе§ЗНаЮга9ИіЛљБОЭМаЮЃЈ3Иіе§ЗНаЮ6ИіГЄЗНаЮЃЉзщГЩЃЌШчЭМЫљЪОПЩвдЭЦжЄЃЎ
ЙщФЩВТЯыЃК
ИљОнЙцТЩЧѓДѓе§ЗНЬхжаКЌгаЖрЩйИіе§ЗНЬхЃЌПЩвдзЊЛЏЮЊ![]() РДЧѓЕУЃЎ
РДЧѓЕУЃЎ
НтЃКЮЪЬтЬНОПЃК
ШчЭМЫљЪОЃК

ЖрЯюЪН![]() аДГЩСНИіећЪНГЫЛ§ЕФаЮЪНЮЊЃКЃЈaЃЋbЃЉЃЈ2aЃЋbЃЉЃЎ
аДГЩСНИіећЪНГЫЛ§ЕФаЮЪНЮЊЃКЃЈaЃЋbЃЉЃЈ2aЃЋbЃЉЃЎ
ГЂЪдНтОіЃК
ШчЭМЃЌAБэЪО1Иі1ЁС1ЕФе§ЗНаЮЃЌМД![]() ЃЌ
ЃЌ
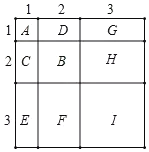
BБэЪО1Иі2ЁС2ЕФе§ЗНаЮЃЌCгыDЧЁКУПЩвдЦДГЩ1Иі2ЁС2ЕФе§ЗНаЮЃЌ
вђДЫBЁЂCЁЂDОЭПЩвдЦДГЩ2Иі2ЁС2ЕФе§ЗНаЮЃЌМДЃК![]() ЃЛ
ЃЛ
GгыHЁЂEгыFКЭIПЩвдЦДГЩ3Иі3ЁС3ЕФе§ЗНаЮЃЌМДЃК![]() ЃЛ
ЃЛ
ЖјећИіЭМаЮЧЁКУПЩвдЦДГЩвЛИіЃЈ1ЃЋ2ЃЋ3ЃЉЁСЃЈ1ЃЋ2ЃЋ3ЃЉЕФДѓе§ЗНаЮЃЌ
вђДЫПЩЕУЃК![]() ЃЎ
ЃЎ
ЙщФЩВТЯыЃК
ИљОнЙцТЩПЩЕУЃК![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ

 ФмСІЦРМлЯЕСаД№АИ
ФмСІЦРМлЯЕСаД№АИ ЬЦгЁЮФЛЏПЮЪБВтЦРЯЕСаД№АИ
ЬЦгЁЮФЛЏПЮЪБВтЦРЯЕСаД№АИЁОЬтФПЁПЙЋдАРягавЛШЫЩшСЫИігЮЯЗЬЏЮЛЃЌгЮПЭжЛашжРвЛУЖе§ЗНЬхїЛзгЃЌШчЙћГіЯж3ЕуЃЌОЭПЩЛёЕУМлжЕ10дЊЕФНБЦЗЃЌУПХзжР1ДЮїЛзгжЛашИЖ1дЊЕФЗбгУЃЎаЁУїдкЬЏЮЛЧАЙлВьСЫКмОУЃЌМЧЯТСЫгЮПЭЕФжаНБЧщПіЃК
гЮПЭ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ХзжРДЮЪ§ | 30 | 20 | 25 | 6 | 16 | 50 | 12 |
жаНБДЮЪ§ | 1 | 0 | 0 | 1 | 0 | 2 | 0 |
ПДСЫаЁУїЕФМЧТМЃЌФугаЪВУДПДЗЈЃП




