题目内容
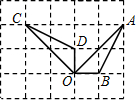
如图①,四边形AEFG和ABCD都是正方形,且点F在AD上,它们的边长分别为12,4.
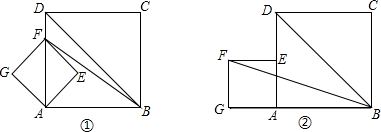
(1)求S△DBF;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的S△DBF;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,S△DBF是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.

(1)求S△DBF;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的S△DBF;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中,S△DBF是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.
(1)∵点F在AD上,
∴AF2=42+42,即AF=4
,
∴DF=12-4
,
∴S△DBF=
DF×AB=
×(12-4
)×12=72-24
;
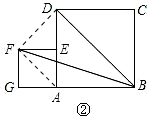 (2)连接DF,AF.
(2)连接DF,AF.
∵由题意易知AF∥BD,
∴四边形AFDB是梯形,
∴△DBF与△ABD等高同底,即BD为两三角形的底,
由AF∥BD,得到平行线间的距离相等,即高相等,
∴S△DBF=S△ABD=72;
(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆,
因为△BFD的边BD=12
,故当F点到BD的距离取得最大、最小值时,S△BFD取得最大、最小值.
如图②所示DF2⊥BD时,S△BFD的最大值=S△BF2D=
×12
•(6
+4
)=120,
S△BFD的最小值=S△BF2D=
×12
•(6
-4
)=24;

∴AF2=42+42,即AF=4
| 2 |
∴DF=12-4
| 2 |
∴S△DBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
 (2)连接DF,AF.
(2)连接DF,AF.∵由题意易知AF∥BD,
∴四边形AFDB是梯形,
∴△DBF与△ABD等高同底,即BD为两三角形的底,
由AF∥BD,得到平行线间的距离相等,即高相等,
∴S△DBF=S△ABD=72;
(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆,
因为△BFD的边BD=12
| 2 |
如图②所示DF2⊥BD时,S△BFD的最大值=S△BF2D=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
S△BFD的最小值=S△BF2D=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |


练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
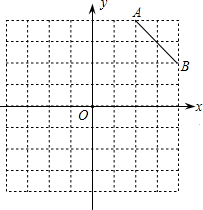 象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.