题目内容

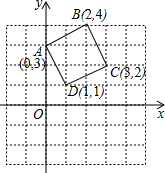
如图，将正五边形ABCDE的C点固定，并依顺时针方向旋转，若要使得新五边形A′B′C′D′E′的顶点D′落在直线BC上，则至少要旋转______°．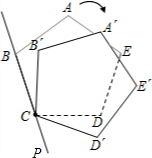
正五边形ABCDE的一个外角的度数=
360°
5
=72°．
即∠DCP=72°，
当将正五边形ABCDE的C点固定，并依顺时针方向旋转，使得新五边形A′B′C′D′E′的顶点D′落在直线BC上，
则∠DAD′等于旋转角，所以旋转的最小角度为∠DCP=72°．
故答案为72°．
练习册系列答案
相关题目
正方形ABCD在坐标系中的位置如图所示，将正方形ABCD绕D点顺时针方向旋转90°后，B点到达的位置坐标为（　　）
A．（-2，2）B．（4，1）C．（3，1）D．（4，0）
如图，四边形ABCD是正方形，△ADE绕着点A旋转90°后到达△ABF的位置，连接EF，则△AEF的形状是（　　）
A．等腰三角形B．直角三角形
C．等腰直角三角形D．等边三角形
如图，已知△ABC的顶点A，B，C的坐标分别是A（-1，-1），B（-4，-3），C（-4，-1）．
（1）作出△ABC关于原点O中心对称的图形△A1B1C1；
（2）写出△A1B1C1各顶点的坐标．
解：（2）A1 （______），B1 （______），C1 （______）．
在一次研究性学习活动中，某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住，保持正方形ABCD不动，顺时针旋转正方形EFGH，如图所示．
（1）小组成员经观察、测量，发现在旋转过程中，有许多有趣的结论．下面是旋转角度小于90°时他们得到的一些猜想：
①ME=MA；
②两张正方形纸片的重叠部分的面积为定值；
③∠MON保持45°不变．
请你对这三个猜想作出判断（正确的在序号后的括号内打上“√”，错误的打上“×”）：
①（　　）；②（　　）；③（　　）
（2）小组成员还发现：（1）中的△EMN的面积S随着旋转角度∠AOE的变化而变化．请你指出在怎样的位置时△EMN的面积S取得最大值．（不必证明）
（3）上面的三个猜想中若有正确的，请选择其中的一个给予证明；若都是错误的，请选择其一说明理由．
如图，△PQR是△ABC经过某种变换后得到的图形．如果△ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标为______．
请阅读下列材料?：
问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=
3
，PC=1．求∠BPC度数的大小和等边三角形ABC的边长．
李明同学的思路是：将△BPC绕点B顺时针旋转60°，画出旋转后的图形（如图2）．连接PP′，可得△P′PB是等边三角形（可证），而△PP′A又是直角三角形（由勾股定理的逆定理可证）．所以∠AP′B=150°，而∠BPC=∠AP′B=150°．进而把AB放在Rt△APB（可证得）中，用勾股定理求出等边△ABC的边长为
7
．问题得到解决．?
[思路分析]首先仔细阅读材料，问题中小明的做法总结起来就是通过旋转固定的角度将已知条件放在同一个（组）图形中进行研究．旋转60度以后BP就成了BP′，PC成了P′A，借助等量关系BP′=PP′，于是△APP′就可以计算了．
解决问题：
请你参考李明同学旋转的思路，探究并解决下列问题：
如图3，在正方形ABCD内有一点P，且PA=
5
，BP=
2
，PC=1．求∠BPC度数的大小和正方形ABCD的边长．
如图①，四边形AEFG和ABCD都是正方形，且点F在AD上，它们的边长分别为12，4．

（1）求S△DBF；
（2）把正方形AEFG绕点A按逆时针方向旋转45°得图②，求图②中的S△DBF；
（3）把正方形AEFG绕点A旋转一周，在旋转的过程中，S△DBF是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由．
四边形ABCD是正方形，△ADF旋转一定的角度后得到△ABE，如图所示，如果AF=4，AB=4
3
，∠F=60°．
（1）指出旋转中心和旋转角度；
（2）求DE的长度；
（3）求∠EBD的度数；
（4）BE与DF的位置关系如何？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网