题目内容
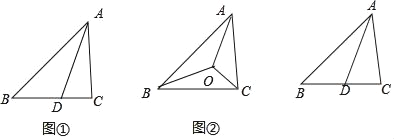
【题目】(发现)(1)如图1,在△ABC中,AD是∠BAC的平分线,对于以下结论:
①AD是△ABC的中线;②S△ABD:S△ACD=AB:AC;③AB:AC=BD:DC,
其中正确的是 (只填序号)
(探究)(2)请你选择(1)中正确的一个选项,简述理由
(应用)(3)如图2,△ABC的三个内角的角平分线相交于点O,且AB=40,BC=48,AC=32,则SABO:S△BCO:S△ACO= : :
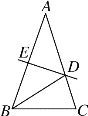
(拓展)(4)在(1)中的条件下,过点D作DE⊥AB于点E,DF⊥AB于点F,连接EF,求证:AD垂直平分EF.
【答案】(1)②③;(2)见解析;(3)5,6,4;(4)证明见解析.
【解析】
(1)根据角平分线的性质和三角形面积公式逐一判断可得;
(2)②由AD平分∠BAC知点D到AB、AC的距离相等,设为h,由S△ABD=![]() ABh,S△ACD=
ABh,S△ACD=![]() ACh可判断结论②;③作AP⊥BC,由S△ABD=
ACh可判断结论②;③作AP⊥BC,由S△ABD=![]() BDAP,S△ACD=
BDAP,S△ACD=![]() CDAP知S△ABD:S△ACD=BD:CD,结合S△ABD:S△ACD=AB:AC可得答案;
CDAP知S△ABD:S△ACD=BD:CD,结合S△ABD:S△ACD=AB:AC可得答案;
(3)作OE⊥AB于E,OF⊥BC于F,OG⊥AC于G,根据角平分线的性质知OE=OF=OG,根据S△ABO=![]() ABOE,S△BCO=
ABOE,S△BCO=![]() BCOF,S△ACO=
BCOF,S△ACO=![]() ACOG可得答案;
ACOG可得答案;
(4)根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明△ADE和△ADF全等,根据全等三角形的可得AE=AF,再利用等腰三角形的证明即可.
(1)正确的是②③,
故答案为:②③.
(2)②∵AD平分∠BAC,
∴点D到AB、AC的距离相等,设为h,
则S△ABD=![]() ABh,S△ACD=
ABh,S△ACD=![]() ACh,
ACh,
∴S△ABD:S△ACD=AB:AC;
③如图1,作AP⊥BC于点P,

则S△ABD=![]() BDAP,S△ACD=
BDAP,S△ACD=![]() CDAP,
CDAP,
∴S△ABD:S△ACD=BD:CD,
又∵S△ABD:S△ACD=AB:AC,
∴AB:AC=BD:CD.
(3)如图2,过点O作OE⊥AB于E,OF⊥BC于F,OG⊥AC于G,
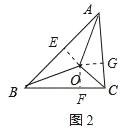
∵AO,BO,CO分别平分∠BAC,∠ABC,∠ACB,
∴OE=OF=OG,
∵S△ABO=![]() ABOE,S△BCO=
ABOE,S△BCO=![]() BCOF,S△ACO=
BCOF,S△ACO=![]() ACOG,
ACOG,
∴SABO:S△BCO:S△ACO=AB:BC:AC=40:48:32=5:6:4,
故答案为:5:6:4;
(4)如图3,

∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
在△ADE和△ADF中,
∵![]() ,
,
∴△ADE≌△ADF(HL),
∴AE=AF,
又∵AD平分∠BAC,
∴AD垂直平分EF.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案