题目内容
【题目】如图,已知A为⊙O外一点,连结OA交⊙O于P,AB为⊙O的切线,B为切点,AP=5㎝,AB= ![]() ㎝,则劣弧
㎝,则劣弧 ![]() 与AB,AP所围成的阴影的面积是.
与AB,AP所围成的阴影的面积是.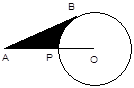
【答案】![]()
【解析】连接OB,因为AB是⊙O的切线,
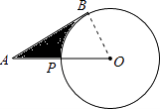
所以∠ABO=90°;
设⊙O的半径为r.由勾股定理得:(5+r)2=( ![]() )2+r2,
)2+r2,
解得r=5cm;在Rt△ABO中,AO=10cm,OB=OP=5cm,
因此∠BOP=60°;
∴S=S△AOB-S扇形OBP= ![]() (cm2).
(cm2).
【考点精析】通过灵活运用勾股定理的概念和切线的性质定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目