Question

【题目】如图，在Rt△ABC中，∠C=90°，AB=60cm，∠A=30°，点D从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，同时点E从点B出发沿BC方向以1cm/秒的速度向点C匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤30）．过点D作DF⊥AC于点F，连接DE，EF．

（1）填空：四边形BEFD是_________；

（2）当t=______时，四边形BEFD能够成为菱形。

（3）当t为何值时？△DEF为直角三角形．

Answer 1

【答案】（1）平行四边形；（2）20；（3）t＝15或24秒时，△DEF为直角三角形．

【解析】

（1）利用t表示出BE的长，利用直角三角形的性质求得DF的长，然后根据平行四边形的判定解答即可；

（2）由菱形的性质可得关于t的方程，解方程即得结果；

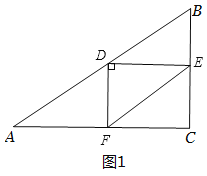
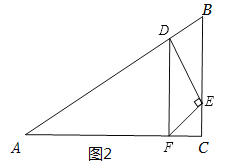
（3）分三种情况：显然∠DFE＜90°；当∠EDF＝90°时，如图1，利用矩形的性质和30°角的直角三角形的性质可得关于t的方程，解方程即得结果；当∠DEF＝90°时，如图2，易得∠BDE＝90°，然后利用30°角的直角三角形的性质解答．

证明：（1）∵∠A＝30°，DF⊥AC，AD＝2t，BE＝t，

∴DF＝AD＝t＝BE，

∵DF⊥AC，BC⊥AC，

∴DF∥BE，且DF＝BE，

∴四边形BEFD是平行四边形；

故答案为：平行四边形；

（2）当BD＝BE时，四边形BEFD能够成为菱形，

此时60﹣2t＝t，∴t＝20，

∴当t＝20s，四边形BEFD能够成为菱形；

故答案为：20；

（3）∵∠DFE＜∠DFC，∴∠DFE＜90°；

当∠EDF＝90°时，如图1，

∵∠ACB＝∠EDF＝∠CFD＝90°，

∴四边形DECF是矩形，

∴DF＝EC＝t，

∵∠C=90°，AB=60cm，∠A=30°，

∴cm，

∴t＝30﹣t，

∴t＝15；

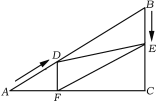
当∠DEF＝90°，如图2，

∵四边形BEFD是平行四边形，

∴BD∥EF，

∴∠BDE＝∠DEF＝90°，且∠B＝60°，

∴∠DEB＝30°，

∴BE＝2BD，

∴2（60﹣2t）＝t，

∴t＝24．

综上所述：当t＝15或24秒时，△DEF为直角三角形．