ĢāÄæÄŚČŻ
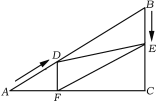
”¾ĢāÄæ”æŹżŃ§æĪÉĻ£¬ÕÅĄĻŹ¦³öŹ¾ĮĖĪŹĢā£ŗČēĶ¼1£¬ĖıߊĪABCDŹĒÕż·½ŠĪ£¬µćEŹĒ±ßBCµÄÖŠµć£®”ĻAEF=90”ć£¬ĒŅEF½»Õż·½ŠĪĶā½Ē”ĻDCGµÄ½ĒĘ½·ÖĻßCFÓŚµćF£¬ĒóÖ¤£ŗAE=EF£®

¾¹żĖ¼æ¼£¬Š”Ć÷Õ¹Ź¾ĮĖŅ»ÖÖÕżČ·µÄ½āĢāĖ¼Ā·£ŗČ”ABµÄÖŠµćM£¬Į¬½ÓME£¬ŌņAM=EC£¬Ņ×Ö¤”÷AME”Õ”÷ECF£¬ĖłŅŌAE=EF£®
ŌŚ“Ė»ł“”ÉĻ£¬Ķ¬Ń§ĆĒ×÷ĮĖ½ųŅ»²½µÄŃŠ¾æ£ŗ
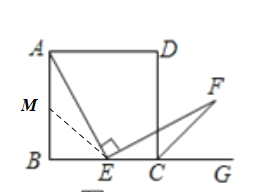
£Ø1£©Š”Ó±Ģį³ö£ŗČēĶ¼2£¬Čē¹ū°Ń”°µćEŹĒ±ßBCµÄÖŠµć”±øÄĪŖ”°µćEŹĒ±ßBCÉĻ£Ø³żB£¬CĶā£©µÄČĪŅāŅ»µć”±£¬ĘäĖüĢõ¼ž²»±ä£¬ÄĒĆ“½įĀŪ”°AE=EF”±ČŌČ»³ÉĮ¢£¬ÄćČĻĪŖŠ”Ó±µÄ¹ŪµćÕżČ·Āš£æČē¹ūÕżČ·£¬Š“³öÖ¤Ć÷¹ż³Ģ£»Čē¹ū²»ÕżČ·£¬ĒėĖµĆ÷ĄķÓÉ£»
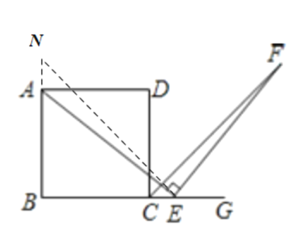
£Ø2£©Š”»ŖĢį³ö£ŗČēĶ¼3£¬µćEŹĒBCµÄŃÓ³¤ĻßÉĻ£Ø³żCµćĶā£©µÄČĪŅāŅ»µć£¬ĘäĖūĢõ¼ž²»±ä£¬½įĀŪ”°AE=EF”±ČŌČ»³ÉĮ¢£®ÄćČĻĪŖŠ”»ŖµÄ¹ŪµćÕżČ·Āš£æČē¹ūÕżČ·£¬Š“³öÖ¤Ć÷¹ż³Ģ£»Čē¹ū²»ÕżČ·£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©ÕżČ·£®Ö¤Ć÷¼ū½āĪö£»£Ø2£©ÕżČ·£®Ö¤Ć÷¼ū½āĪö.
”¾½āĪö”æ
£Ø1£©ŌŚ![]() ÉĻČ”Ņ»µć
ÉĻČ”Ņ»µć![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬øł¾ŻŅŃÖŖĢõ¼žĄūÓĆ
£¬øł¾ŻŅŃÖŖĢõ¼žĄūÓĆ![]() ÅŠ¶Ø
ÅŠ¶Ø![]() £¬ŅņĪŖČ«µČČż½ĒŠĪµÄ¶ŌÓ¦±ßĻąµČ£¬ĖłŅŌ
£¬ŅņĪŖČ«µČČż½ĒŠĪµÄ¶ŌÓ¦±ßĻąµČ£¬ĖłŅŌ![]() £®
£®
£Ø2£©ŌŚ![]() µÄŃÓ³¤ĻßÉĻČ”Ņ»µć
µÄŃÓ³¤ĻßÉĻČ”Ņ»µć![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬øł¾ŻŅŃÖŖĄūÓĆ
£¬øł¾ŻŅŃÖŖĄūÓĆ![]() ÅŠ¶Ø
ÅŠ¶Ø![]() £¬ŅņĪŖČ«µČČż½ĒŠĪµÄ¶ŌÓ¦±ßĻąµČ£¬ĖłŅŌ
£¬ŅņĪŖČ«µČČż½ĒŠĪµÄ¶ŌÓ¦±ßĻąµČ£¬ĖłŅŌ![]() £®
£®
½ā£ŗ£Ø1£©ÕżČ·£®
Ö¤Ć÷£ŗŌŚ![]() ÉĻČ”Ņ»µć
ÉĻČ”Ņ»µć![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() ŹĒĶā½ĒĘ½·ÖĻߣ¬
ŹĒĶā½ĒĘ½·ÖĻߣ¬
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() £®
£®
£Ø2£©ÕżČ·£®
Ö¤Ć÷£ŗČēĶ¼Ź¾£¬ŌŚ![]() µÄŃÓ³¤ĻßÉĻČ”Ņ»µć
µÄŃÓ³¤ĻßÉĻČ”Ņ»µć![]() £¬Ź¹
£¬Ź¹![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
![]() £¬
£¬
![]() £¬
£¬
![]() Ę½·Ö
Ę½·Ö![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() ĖıߊĪ
ĖıߊĪ![]() ŹĒÕż·½ŠĪ£¬
ŹĒÕż·½ŠĪ£¬
![]() £¬
£¬
![]() £¬
£¬
¼“![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
![]() £®
£®

 ½Ż¾¶ŃµĮ·¼ģ²ā¾ķĻµĮŠ“š°ø
½Ż¾¶ŃµĮ·¼ģ²ā¾ķĻµĮŠ“š°ø Š”·ņ×ÓČ«Äܼģ²āĻµĮŠ“š°ø
Š”·ņ×ÓČ«Äܼģ²āĻµĮŠ“š°ø”¾ĢāÄæ”æÉś»īÓėŹżŃ§
ČÕ | Ņ» | ¶ž | Čż | ĖÄ | Īå | Įł |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
£Ø1£©Ä·Ķ¬Ń§ŌŚÄ³ŌĀµÄČÕĄśÉĻȦ³ö2”Į2øöŹż£¬Õż·½ŠĪµÄ·½æņÄŚµÄĖÄøöŹżµÄŗĶŹĒ48£¬ÄĒĆ“ÕāĖÄøöŹżŹĒ_______.
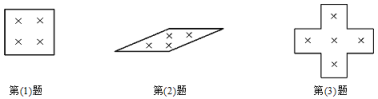
£Ø2£©ĄöŅ²ŌŚÉĻĆęµÄČÕĄśÉĻȦ³ö2”Į2øöŹż£¬Š±æņÄŚµÄĖÄøöŹżµÄŗĶŹĒ46£¬ŌņĖüĆĒ·Ö±šŹĒ_____.
£Ø3£©ĄņŅ²ŌŚČÕĄśÉĻȦ³ö5øöŹż£¬³ŹŹ®×ÖæņŠĪ£¬ĖüĆĒµÄŗĶŹĒ55£¬ŌņÖŠ¼äµÄŹżŹĒ______.
£Ø4£©Ä³ŌĀÓŠ5øöŠĒĘŚČÕµÄŗĶŹĒ75£¬ŌņÕāøöŌĀÖŠ×īŗóŅ»øöŠĒĘŚČÕŹĒ______ŗÅ£æ