题目内容
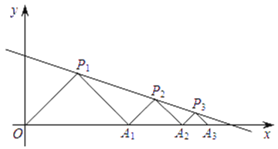
【题目】如图,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的动点(点
上的动点(点![]() 不与点
不与点![]() 重合),直线
重合),直线![]() 经过点
经过点![]() ,并与
,并与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(1)求![]() 的函数表达式;
的函数表达式;
(2)当![]() 时,
时,
①求点![]() 的坐标;
的坐标;
②求![]() .
.
(3)将点![]() 的横坐标记为
的横坐标记为![]() ,在点
,在点![]() 移动的过程中,直接写出
移动的过程中,直接写出![]() 的范围.
的范围.
【答案】(1)![]() 的表达式为
的表达式为![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]()
【解析】
(1)先设![]() 的方程为y=kx+b,再根据两点确定一条直线,将已知坐标(0,2)、(6,-2)带入方程计算即可;
的方程为y=kx+b,再根据两点确定一条直线,将已知坐标(0,2)、(6,-2)带入方程计算即可;
(2)①将k值带入![]() 方程后,联立方程组即可算出M的坐标;
方程后,联立方程组即可算出M的坐标;
②通过A点与P点纵坐标相同,即可算出P的具体坐标,再根据坐标算出三角形的底和高,应用三角形面积公式即可求出;
(3)由P点的活动范围是AB之间,大致明确![]() 的大小变化,再根据相似三角形算出N点坐标,带入
的大小变化,再根据相似三角形算出N点坐标,带入![]() ,即可算出
,即可算出![]() 的范围.
的范围.
解:(1)设![]() 的表达式为:
的表达式为:![]() ,将点
,将点![]() 和
和![]() 代入,
代入,
求得![]() 的表达式为:
的表达式为:![]() .
.
(2)当![]() 时,
时,
①求得![]() 的表达式为:
的表达式为:![]() ,
,
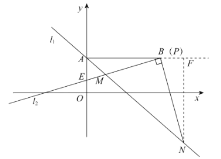
解方程组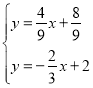 ,求得交点
,求得交点![]() .
.
②当![]() 时,有
时,有![]() ,解得
,解得![]() ,∴
,∴![]() .
.
点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
∴![]() .
.
(3)![]()
由题![]() 恒过点
恒过点![]() ,
,![]() 与线段
与线段![]() 有交点,
有交点,
∵点![]() 的运动范围是线段
的运动范围是线段![]() (点
(点![]() 不与点
不与点![]() 重合),
重合),
①点![]() 的横坐标随着
的横坐标随着![]() 变小而变小,即
变小而变小,即![]() 趋于0.
趋于0.
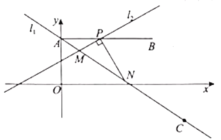
②当![]() 过点
过点![]() 时,此时点
时,此时点![]() 与点
与点![]() 重合,如图所示,
重合,如图所示,
过点![]() 作
作![]() ,
,
∴![]() .∴
.∴![]() .
.
设点![]() ,则
,则![]() ,
,![]() .
.
∵![]() 过点
过点![]() ,其表达式为
,其表达式为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
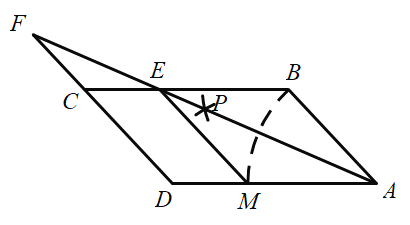
∴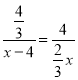 ,
,
∴![]() ,即
,即![]() .
.
∴![]() .
.

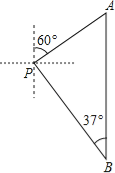
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.