题目内容
【题目】在一个不透明的口袋中放入
个大小形状几乎完全相同实验用的鸡蛋，鸡蛋的质量有微小的差距（用手感觉不到差异），质量分别为
、
、
克，已知随机的摸出一个鸡蛋，摸到克和克的鸡蛋的概率是相等的．
（1）求这四个鸡蛋质量的众数和中位数
（2）小明做实验需要拿走一个鸡蛋，芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后，剩下的三个鸡蛋质量的中位数是多少？
②假设小明拿走的鸡蛋质量为克，芳芳随机的拿出一个鸡蛋后又放回，之后再随机的拿出一个鸡蛋，请用树状图求芳芳两次拿到都是克的鸡蛋的概率？
【答案】（1）因此鸡蛋质量的众数为
，中位数也是．（2）①；②
【解析】
（1）因为
个鸡蛋有三个质量数，所以必然有两个鸡蛋的质量是相等的，又根据摸到
克的鸡蛋和
克的鸡蛋概率相等，从而可得答案，
（2）①若小明分别拿走的是不同的鸡蛋，分析剩下的鸡蛋，可得到答案，
②利用树状图得到两次拿走50克鸡蛋的机会，从而可得答案．
解（1）因为个鸡蛋有三个质量数，所以必然有两个鸡蛋的质量是相等的，所以四个鸡蛋的质量可能为、、、；、、、；、、、．又根据摸到克的鸡蛋和克的鸡蛋概率相等，
我们从前面数据分析可知，摸到鸡蛋的的概率分别是
，，
，
所以我们知道四个鸡蛋的质量数为、、、；
因此鸡蛋质量的众数为，中位数也是．
（2）①若小明拿走的是49,剩下的是,,，此时中位数是50，
若小明拿走的是50,剩下的是49、,，此时中位数是50，
若小明拿走的是51,剩下的是49,,,此时中位数是50，
所以小明拿走一个鸡蛋，不管小明拿走的鸡蛋质量是多少，剩下鸡蛋的中位数都是；
②画树状图如下：
共有
种情况：，；，；，；，；，；，；，；，，，．其中两次拿到克的情况有四种，所以两次都拿到克鸡蛋的概率为
新思维假期作业暑假吉林大学出版社系列答案
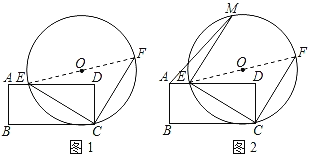
蓝天教育暑假优化学习系列答案
【题目】如图，
是
与弦
所围成图形的外部的一定点，
是弦上的一动点，连接
交于点
．已知
，设，
两点间的距离为
，，两点间的距离为
，，两点间的距离为
．
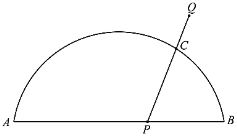
小石根据学习函数的经验，分别对函数
，
随自变量
的变化而变化的规律进行了探究，下面是小石的探究过程，请补充完整：
（1）按照下表中自变量的值进行取点、画图、测量分别得到了，与的几组对应值：
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
（2）在同一平面直角坐标系
中，描出补全后的表中各组数值所对应的点
，
，并画出函数，的图象；
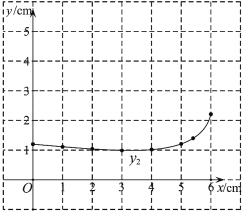
（3）结合函数图象，解决问题：当为的中点时，
的长度约为______
．
