题目内容
【题目】某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场,下表是他的技术统计.
场次 | 对阵甲队 | 对阵乙队 | ||
得分(分) | 失误(次) | 得分(分) | 失误(次) | |
第一场 | 25 | 2 | 27 | 3 |
第二场 | 30 | 0 | 31 | 1 |
第三场 | 27 | 3 | 20 | 2 |
第四场 | 26 | 2 | 26 | 4 |
(1)他在对阵甲队和乙队的各四场比赛中,平均每场得分分别是多少?
(2)利用方差判断他在对阵哪个队时得分比较稳定;
(3)根据上表提供的信息,判断他在对阵哪个队时总体发挥较好,简要说明理由.
【答案】(1)他对阵甲队的平均每场得分为27分,对阵乙队的平均每场得分为26分;(2)他在对阵甲队时得分比较稳定;(3)他在对阵甲队时总体发挥较好,理由见解析.
【解析】
(1)根据平均数的计算公式分别进行计算即可;
(2)根据方差公式进行计算,再根据方差的意义即可得出答案;
(3)根据失误次数和方差的意义即可得出答案.
(1)解:![]() =
=![]() =27,
=27,![]() =
=![]() =26.
=26.
答:他对阵甲队的平均每场得分为27分,对阵乙队的平均每场得分为26分.
(2)解:![]() =
=![]() =3.5,
=3.5,
![]() =
=![]() =15.5.
=15.5.
由可知![]() ,他在对阵甲队时得分比较稳定.
,他在对阵甲队时得分比较稳定.
(3)解:他在对阵甲队时总体发挥较好.
理由:由![]() 可知他对阵甲队时平均得分较高;
可知他对阵甲队时平均得分较高;
由![]() 可知,他在对阵甲队时得分比较稳定;
可知,他在对阵甲队时得分比较稳定;
计算得他对阵甲队平均失误为1.75次,对阵乙队平均失误为2.5次,
由1.75次<2.5次可知他在对阵甲队时失误较少.

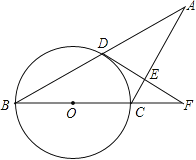
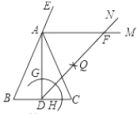
【题目】如图,![]() 是
是![]() 与弦
与弦![]() 所围成图形的外部的一定点,
所围成图形的外部的一定点,![]() 是弦
是弦![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
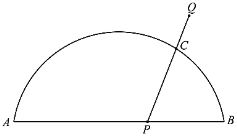
小石根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量分别得到了
的值进行取点、画图、测量分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
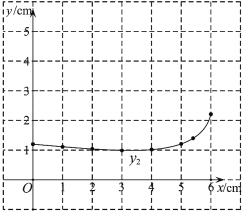
(3)结合函数图象,解决问题:当![]() 为
为![]() 的中点时,
的中点时,![]() 的长度约为______
的长度约为______![]() .
.