题目内容
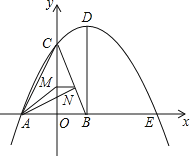
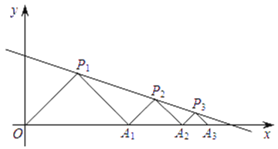
【题目】如图，在平面直角坐标系中，
，
，
，．．．都是等腰直角三角形，其直角顶点
，
，
，．．．均在直线
上，设，，，．．．的面积分别为
，
，
，．．．，依据图形所反映的规律，S2020＝__________．
【答案】
【解析】
过点
、
、
作x轴的垂线段，在结合等腰
，可推导出的坐标；同理，可得到、
…的坐标；最后通过寻找这些坐标之间的规律，得到最终结果
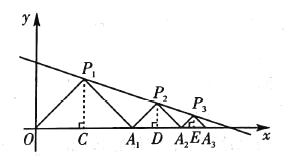
如图，分别过点、、作x轴的垂线段，垂足分别为C，D ，E． P(3,3)，且，是等腰直角三角形，
∴OC=C
=C=3，则D=a，
∴OD=6+a，
∴点的坐标为(6+a，a) a.
将点的坐标代入
中，得
(6+a)+4=a，解得a=
∴
=2a=3，D= ．
同理求得
=
，
= ．
∵
=
×6×3=9，
=×3× =
，
=××
=
，…，∴
=
练习册系列答案
阅读快车系列答案
相关题目
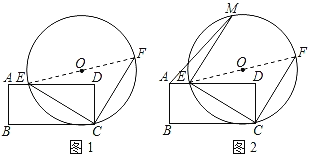
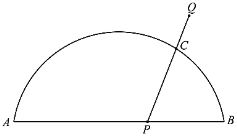
【题目】如图，
是
与弦
所围成图形的外部的一定点，
是弦上的一动点，连接
交于点
．已知
，设，
两点间的距离为
，，两点间的距离为
，，两点间的距离为
．
小石根据学习函数的经验，分别对函数
，
随自变量
的变化而变化的规律进行了探究，下面是小石的探究过程，请补充完整：
（1）按照下表中自变量的值进行取点、画图、测量分别得到了，与的几组对应值：
| 0 | 1 | 2 | 3 | 4 | 5 | 5.40 | 6 |
| 4.63 | 3.89 | 2.61 | 2.15 | 1.79 | 1.63 | 0.95 | |
| 1.20 | 1.11 | 1.04 | 0.99 | 1.02 | 1.21 | 1.40 | 2.21 |
（2）在同一平面直角坐标系
中，描出补全后的表中各组数值所对应的点
，
，并画出函数，的图象；
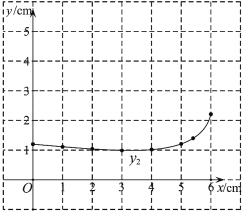
（3）结合函数图象，解决问题：当为的中点时，
的长度约为______
．
