题目内容
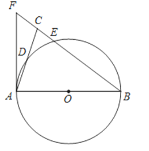
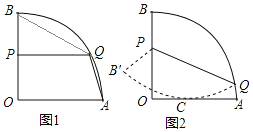
【题目】如图1,扇形OAB的半径为4,∠AOB=90°,P是半径OB上一动点,Q是![]() 上一动点.
上一动点.
(1)连接AQ、BQ、PQ,则∠AQB的度数为 ;
(2)当P是OB中点,且PQ∥OA时,求![]() 的长;
的长;
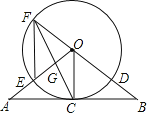
(3)如图2,将扇形OAB沿PQ对折,使折叠后的![]() 恰好与半径OA相切于点C.若OP=3,求点O到折痕PQ的距离.
恰好与半径OA相切于点C.若OP=3,求点O到折痕PQ的距离.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图,补全图形,运用圆内接四边形的性质求解即可;
(2)要想求![]() 弧长,就得求
弧长,就得求![]() 所对的圆心角的度数,所以要连接OQ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出∠1=30°,再利用平行线截得内错角相等得出∠2的度数,代入弧长公式计算即可.
所对的圆心角的度数,所以要连接OQ,构成圆心角,利用直角三角形直角边是斜边的一半,则这条直角边所对的锐角为30°求出∠1=30°,再利用平行线截得内错角相等得出∠2的度数,代入弧长公式计算即可.
(3)先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=![]() OO′=
OO′=![]() .
.
(1)补全图形如图所示,
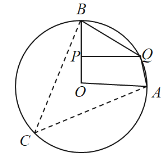
∵∠AOB=90°,
∴∠BCA=45°,
∵四边形ACBQ是圆内接四边形,
∴∠AQB+∠C=180°,
∴∠AQB=180°-∠C=135°
故答案为:135°;
(2)如图1,连接OQ,
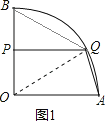
∵扇形OAB的半径为4且P是OB中点,
∴OP=2,OQ=4,
∵PQ∥OA,
∴∠BPQ=∠AOB=90°,
∴∠OQP=30°,
∴∠AOQ=∠OQP=30°,
∴![]() 的长=
的长=![]() =
=![]() π;
π;
(3)如图2,找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,ON,
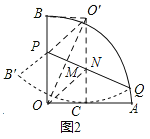
则OM=O′M,OO′⊥PQ,O′P=OP=3,点O′是![]() 所在圆的圆心,
所在圆的圆心,
∴O′C=OB=4,
∵折叠后的弧QB′恰好与半径OA相切于C点,
∴O′C⊥AO,
∴O′C∥OB,
∴∠POO'=∠CO'M=∠PO'M,
∵∠PMO'=∠QMO'=90°,
∴∠O'PM=∠MNO',
∴O'P=O'N=OP=3,
∴四边形OPO'N是平行四边形,
∴O'P=ON,
∵O与O'关于PQ对称,
∴ON=O'N=3,
∴BP=CN=4﹣3=1,
∵PN⊥OO',
∴∠MNO'=∠MNO,
∴∠BPO'=∠CNO,
∴△O'BP≌△OCN(SAS),
∴∠O'BP=∠OCN=90°,
∴四边形OCO′B是矩形,
在Rt△O′BP中,O′B=![]() =2
=2![]() ,
,
在Rt△OBO′中,OO′=![]() =2
=2![]() ,
,
∴OM=![]() OO′=
OO′=![]() ×2
×2![]() =
=![]() ,
,
即O到折痕PQ的距离为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案