题目内容
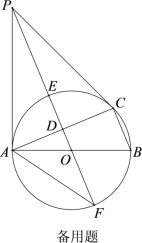
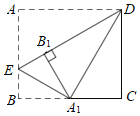
【题目】如图1,直线![]() x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴交于点A,与x轴交于点D,直线AB交x轴于点B,将△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
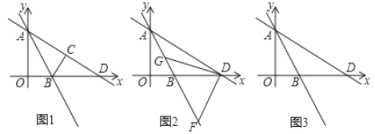
(1)求OB的长;
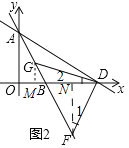
(2)如图2,F,G是直线AB上的两点,若△DFG是以FG为斜边的等腰直角三角形,求点F的坐标;
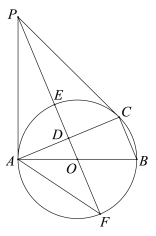
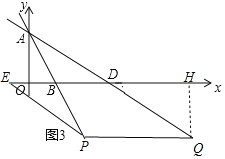
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P,Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
【答案】(1)OB=3;(2)F(6,-6);(3)E(-2,0).
【解析】
(1)设BC=OB=x,则BD=8-x,在Rt△BCD中,根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)作GM⊥x轴于M,FN⊥x轴于N,由△DMG≌△FND(AAS),推出GM=DN,DM=FN,设GM=DM=m,DM=FN=n,根据G、F在直线AB上,构建方程组即可解决问题;
(3)如图,设Q![]() ,因为PQ∥x轴,且点P在直线y=-2x+6上,推出P
,因为PQ∥x轴,且点P在直线y=-2x+6上,推出P![]() ,PQ=
,PQ=![]() ,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,构建方程即可解决问题.
,作QH⊥x轴于H.由勾股定理可知:QH:DH:DQ=3:4:5,构建方程即可解决问题.
解:(1)对于直线![]() ,令x=0,得到y=6,可得A(0,6),
,令x=0,得到y=6,可得A(0,6),
令y=0,得到x=8,可得D(8,0),
![]() AC=AO=6,OD=8,AD
AC=AO=6,OD=8,AD![]() ,
,
![]()
![]()
设BC=OB=x,则BD=![]() ,
,
在Rt△BCD中,∵BC2+CD2=BD2,
![]()
![]()
![]() x=3,
x=3,
![]() OB=3.
OB=3.
(2)设直线AB的解析式为y=kx+6(k≠0),
![]() OB=3,即B(3,0),
OB=3,即B(3,0),
![]() 把B(3,0)代入y=kx+6得,
把B(3,0)代入y=kx+6得,
![]() 3k+6=0,
3k+6=0,
![]()
![]() 直线AB的解析式为y=-2x+6,
直线AB的解析式为y=-2x+6,
作GM⊥x轴于M,FN⊥x轴于N,![]()
![]() △DFG是等腰直角三角形,
△DFG是等腰直角三角形,
![]() DG=FD,∠GDF=90°,
DG=FD,∠GDF=90°,
![]()
![]()
![]()
![]()
在△DMG和△FND中,

![]()
![]() GM=DN,DM=FN,设GM=DN=m,DM=FN=n,
GM=DN,DM=FN,设GM=DN=m,DM=FN=n,
![]()
![]() G、F在直线AB上,
G、F在直线AB上,
则: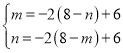 ,
,
解得:![]()
![]() ON=OD-DN=8-2=6,
ON=OD-DN=8-2=6,
![]()
![]()
![]() F(6,-6).
F(6,-6).
(3)如图,设Q(a,![]() ),
),
![]() PQ//x轴,且点P在直线
PQ//x轴,且点P在直线![]() 上,
上,
![]() P(
P(![]() ),
),
![]() PQ
PQ![]() ,作QH⊥x轴于H.
,作QH⊥x轴于H.
![]()
∴![]() ,
,
![]() ,
,
![]()
![]()
![]()
由勾股定理可知:QH:DH:DQ=3:4:5,
![]() 四边形PQDE为菱形,
四边形PQDE为菱形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Q(16,-6),P(6,-6),
Q(16,-6),P(6,-6),
![]()
![]()
![]()

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案