题目内容
【题目】用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:m),如果在离水面竖直距离为h(单校:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H—h).
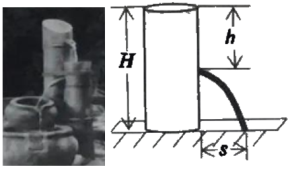
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高h cm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.
【答案】(1)![]() ,当
,当![]() 时,
时,![]() ;(2)
;(2)![]() 或
或![]() ;(3)垫高的高度为16cm,小孔离水面的竖直距离为18cm
;(3)垫高的高度为16cm,小孔离水面的竖直距离为18cm
【解析】
(1)将s2=4h(20-h)写成顶点式,按照二次函数的性质得出s2的最大值,再求s2的算术平方根即可;
(2)设存在a,b,使两孔射出水的射程相同,则4a(20-a)=4b(20-b),利用因式分解变形即可得出答案;
(3)设垫高的高度为m,写出此时s2关于h的函数关系式,根据二次函数的性质可得答案.
解:(1)∵s2=4h(H-h),
∴当H=20时,s2=4h(20-h)=-4(h-10)2+400,
∴当h=10时,s2有最大值400,
∴当h=10时,s有最大值20cm.
∴当h为何值时,射程s有最大值,最大射程是20cm;
故答案为:最大射程是20cm.
(2) ∵s2=4h(20-h),
设存在a,b,使两孔射出水的射程相同,则有:
4a(20-a)=4b(20-b),
∴20a-a2=20b-b2,
∴a2-b2=20a-20b,
∴(a+b)(a-b)=20(a-b),
∴(a-b)(a+b-20)=0,
∴a-b=0或a+b-20=0,
∴a=b或a+b=20.
故答案为:a=b或a+b=20.
(3)设垫高的高度为m,则![]()
∴当![]() 时,
时,![]()
∴![]() 时,此时
时,此时![]()
∴垫高的高度为16cm,小孔离水面的竖直距离为18cm.
故答案为:垫高的高度为16cm,小孔离水面的竖直距离为18cm.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案