题目内容
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
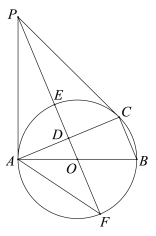
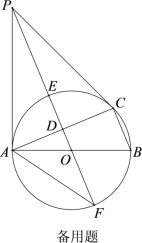
【答案】(1)见解析;(2)见解析;(3)DE=![]() .
.
【解析】
(1)先判断出PA=PC,得出∠PAC=∠PCA,再判断出∠ACB=90°,得出∠CAB+∠CBA=90°,再判断出∠PCA+∠CAB=90°,得出∠CAB+∠PAC=90°,即可得出结论;
(2)先判断出Rt△AOD∽Rt△POA,得出OA2=OPOD,进而得出
![]() ,,即可得出结论;
,,即可得出结论;
(3)在Rt△ADF中,设AD=a,得出DF=3a.![]() ,AO=OF=3a-4,最后用勾股定理得出OD2+AD2=AO2,即可得出结论.
,AO=OF=3a-4,最后用勾股定理得出OD2+AD2=AO2,即可得出结论.
(1)证明∵D是弦AC中点,∴OD⊥AC,∴PD是AC的中垂线,∴PA=PC,∴∠PAC=∠PCA.
∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠CBA=90°.
又∵∠PCA=∠ABC,∴∠PCA+∠CAB=90°,∴∠CAB+∠PAC=90°,即AB⊥PA,∴PA是⊙O的切线;
(2)证明:由(1)知∠ODA=∠OAP=90°,
∴Rt△AOD∽Rt△POA,∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,即
,即![]() .
.
(3)解:在Rt△ADF中,设AD=a,则DF=3a.![]() ,AO=OF=3a-4.
,AO=OF=3a-4.
∵![]() ,即
,即![]() ,解得
,解得![]() ,∴DE=OE-OD=3a-8=
,∴DE=OE-OD=3a-8=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目