题目内容
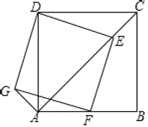
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,请直接写出ME的长.
【答案】(1)见解析;(2)AE+AG==4![]() ;(3)EM=
;(3)EM=![]() .
.
【解析】
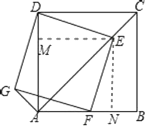
(1)如图,作EM⊥AD于M,EN⊥AB于N.只要证明△EMD≌△ENF即可解决问题;
(2)只要证明△ADG≌△CDE,可得AG=EC即可解决问题;
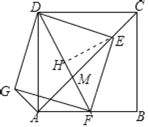
(3)如图,作EH⊥DF于H.想办法求出EH,HM即可解决问题;
(1)如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF,
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形.
(2)∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE,
∴AG=CE,
∴AE+AG=AE+EC=AC=![]() AD=4
AD=4![]() .
.
(3)如图,作EH⊥DF于H.
∵四边形ABCD是正方形,
∴AB=AD=4,AB∥CD,
∵F是AB中点,
∴AF=FB
∴DF=![]() ,
,
∵△DEF是等腰直角三角形,EH⊥AD,
∴DH=HF,
∴EH=![]() DF=
DF=![]() ,
,
∵AF∥CD,
∴AF:CD=FM:MD=1:2,
∴FM=![]() ,
,
∴HM=HF﹣FM=![]() ,
,
在Rt△EHM中,EM=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某次篮球联赛共有十支队伍参赛,部分积分表如下.根据表格提供的信息解答下列问题:
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
A | 18 | 14 | 4 | 32 |
B | 18 | 11 | 7 | 29 |
C | 18 | 9 | 9 | 27 |
(1)列一元一次方程求出胜一场、负一场各积多少分?
(2)某队的胜场总积分能等于它的负场总积分吗?若能,试求胜场数和负场数;若不能,说出理由.
(3)试就某队的胜场数求出该队的负场总积分是它的胜场总积分的正整数倍的情况?