题目内容
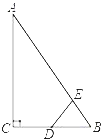
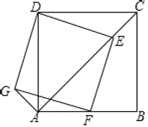
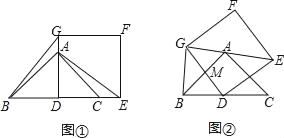
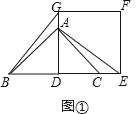
【题目】如图①,AD为等腰直角△ABC的高,点A和点C分别在正方形DEFG的边DG和DE上,连接BG、AE.
(1)求证:BG=AE;
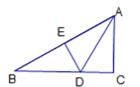
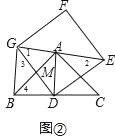
(2)将正方形DEFG绕点D旋转,当线段EG经过点A时,(如图②所示)
①求证:BG⊥GE;
②设DG与AB交于点M,若AG=6,AE=8,求DM的长.
【答案】(1)证明见解析;(2)①证明见解析;②DM=![]() ,
,
【解析】试题分析:(1)如图①,根据等腰直角三角形的性质得AD=BD,再根据正方形的性质得∠GDE=90°,DG=DE,则可根据“SAS“判断△BDG≌△ADE,于是得到BG=AE;
(2)①如图②,先判断△DEG为等腰直角三角形得到∠1=∠2=45°,再由△BDG≌△ADE得到∠3=∠2=45°,则可得∠BGE=90°,所以BG⊥GE;
②由AG=6,则AE=8,即GE=14,利用等腰直角三角形的性质得DG=![]() GE=7
GE=7![]() ,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=
,由(1)的结论得BG=AE=8,则根据勾股定理得AB=10,接着由△ABD为等腰直角三角形得到∠4=45°,BD=![]() AB=5
AB=5![]() ,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
,然后证明△DBM∽△DGB,则利用相似比可计算出DM;
试题解析:
(1)证明:如图①,
∵AD为等腰直角△ABC的高,
∴AD=BD,
∵四边形DEFG为正方形,
∴∠GDE=90°,DG=DE,
在△BDG和△ADE中
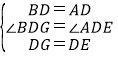 ,
,
∴△BDG≌△ADE,
∴BG=AE;
(2)①证明:如图②,
∵四边形DEFG为正方形,
∴△DEG为等腰直角三角形,
∴∠1=∠2=45°,
由(1)得△BDG≌△ADE,
∴∠3=∠2=45°,
∴∠1+∠3=45°+45°=90°,即∠BGE=90°,
∴BG⊥GE;
②解:∵AG=6,则AE=8,即GE=14,
∴DG=![]() GE=7
GE=7![]() ,
,
∵△BDG≌△ADE,
∴BG=AE=8,
在Rt△BGA中,AB=![]() =10,
=10,
∵△ABD为等腰直角三角形,
∴∠4=45°,BD=![]() AB=5
AB=5![]() ,
,
∴∠3=∠4,
而∠BDM=∠GDB,
∴△DBM∽△DGB,
∴BD:DG=DM:BD,即 5![]() :7
:7![]() =DM:5
=DM:5![]() ,
,
∴DM=![]() ,
,

 金钥匙试卷系列答案
金钥匙试卷系列答案